Амплитуда фаза отговор (АРС) - studopediya
Ако промяната на ъгловата честота со на входния сигнал от 0 до ∞. вектора в комплекса равнина ще варира по размер и да се върти по отношение на реалната ос.
Амплитудна фаза характеристика на канала за свръзка (крива пътуване във времето), изготвен в комплексната равнина на честота вектора на функцията при смяна на честотата ъгъл ωvhodnogo сигнал от 0 до ∞.
APC показва относителна промяна в амплитудата на хармонична сигнал и фаза на системата предава връзка или промяна на ъгловата честота со на от 0 до ∞.
Както primerarassmotrim сложна функция трансфер честота и амплитуда фаза характеристика на първо закъснение за елемент от които се характеризира чрез следното уравнение:
където Т - времеконстанта;
K - печалба.
За Формула предавателната функция честота комплекс е необходимо за решаване на уравнението за изходния сигнал и се разделят на входния сигнал:
За да се определи амплитуда и фаза на отговор, предавателната функция комплекс честота трябва да бъде изразено като сумата от реални и въображаеми части:
Зависимост от абсолютната стойност на функцията за трансфер на ъгловата честота определя честотната (честота отговор) и зависимостта на фазата на предавателната функция определя отговор фаза връзка (PFC):
Изразяване ωT стойност от второто уравнение, и замествайки в уравнението АРС, ние получаваме израз на функцията на модула за трансфер честота през фаза:
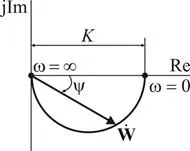
От тази формула следва, че APC забавяне първи ред елемент представлява полукръг. диаметърът на която е разположена върху реалната ос и съответства на печалба K апериодична връзката. С увеличаване на честотата на честотата на вектор функция модул блок се намалява поради въртенето на вектора на предавателната функция на часовниковата стрелка. В безкрайна честота вектор модул клони към нула, а фаза достига - 90º.
Логаритмични честотни характеристики (LCHH).
Комплекс функция трансфер честота при смяна на честотата на ъгъла могат да бъдат представлявани от две реални характеристики: амплитуда честота и фаза честота. Недостатъците на тези характеристики е трудността при тяхното представителство в широк диапазон на изменение на ъгловата честота. Изчисляване и изграждане на тези характеристики значително опростено чрез използване на логаритмична скала.
логаритмичната амплитуда честота характеристика (LACHH) показва как промени в логаритмична скала като функция на ъгловото честотата на хармонична сигнал амплитуда на предадения връзка или система по отношение на входния сигнал на амплитудата хармонична. За количествено определяне на логаритмична ордината LACHH използва мощност усилване единица 1bel хармоничен сигнал [В]. използвана в акустика.
Логаритмична единица 1bel мощност усилвателна [В], характеризиращ се с усилване на мощността на сигнала 10 пъти. хармоничен сигнал мощност е пропорционална на квадрата на амплитудата му, така че В 1 съответства на печалбата в амплитудата на сигнала пъти. На практика се използва кратни 1 децибели [db] В = 0.1, съответната мощност усилване на сигнала по време и увеличаване на амплитудата на пъти.
Логаритми lgω ъглова честота, изразена в продължение на десетилетия; 01 декември съответства на увеличение на честотата на 10 пъти, lgω = 0 съответства на со = 1 и -1.
Аналитичният експресията LACHH G (ω) се определя, като логаритъма на квадрат модула на комплекс честота функцията и се умножи по 10 за прехвърляне на под-кратни на амплификация на мощност - децибели:
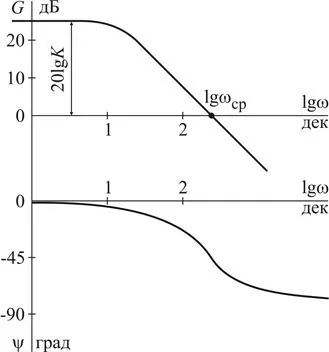
График LAHCH изгради в логаритмични координати. Усилване на силата на сигнала в db, нанесени на ординатата и логаритмична нарастване на честотата, в продължение на десетилетия - по абсцисата. характеристики място над усилване ордината описва амплитудата и силата на хармоничен сигнал на изходния блок или системата по отношение на входа. Ако характеристиката или част разположен под оста х, това съответства на отслабване на амплитудата на сигнала и силата. В точката на пресичане на характеристика оста х, наречен прекъсваща честота ωsr на.
ω = ωsr; Þ ,
Терминът "изключване честотата" представлява хармонична честота на сигнала над която амплитудата на сигнала на изхода устройството или системата става по-ниска, отколкото на входа (изрезка случва амплитуда и силата на сигнала).
Логаритмична фаза отговор (LFCHH) - тази зависимост от относителната фаза на хармонични промени на сигнала по време на предаване връзка или система на логаритъма на честотата на ъгъл. В графиката промяната във фаза ψ, изразена в градуси или радиани, нанасят по ординатата. Логаритмична честота в продължение на десетилетия, нанесени по абсцисата. логаритмична амплитуда и фаза отговор обикновено се комбинират координатната LGW, или има един под друг.
характеристики на изображението в логаритмични координати се сравнява с конвенционалния честотната характеристика следните предимства:
1. Формата на логаритмични честотни характеристики не зависят от параметрите на връзката: печалба и времеконстанта; форма се определя от характеристиките на честотата на предавателната функция.
2. LACHH изместен нагоре по вертикалната ос с увеличаване на нивото на печалба, което е спад - с намаляване на печалба.
3. LACHH LFCHH и изместена в ляво по хоризонталната ос се увеличава с времето постоянно единица, в дясно - с намаляване на времето постоянно.
Използвайки Особености типични единици намалява всички изчисления за изчисляване на характеристиките на две координати: логаритъма на печалбата и логаритъма на реципрочната стойност на времеконстантата, наречен честота или прекъсваща честота конюгирането. Честотните характеристики на устройството свързване определя местоположението на функции на абсцисата. Обикновено LAHCH строителство работи по опростен начин, чрез заместване на действителните характеристики на линейните сегменти. При изграждането на работа LFHCH шаблони.