AC 54 разклонена верига
В практиката често се използва с разклонена верига, която е необходима за изчисляване на тока във всички клонове, и на тока на цялата верига, както и като активна, реактивна и активната мощност на веригата.
Верига от две паралелни клонове.
Да разгледаме прост AC верига, съдържащ две успоредни клонове със серия съпротивления и рулони и свързани към източник на синусоидално напрежение (ris.151). В съответствие със закона за запазване на такса мощност, токът в права част от веригата е сумата от токовете в паралелни клонове.
Във всеки клон ток ще изостане напрежението върху крака (вж. § 52), както и напрежението в общите клоните. Ето защо, се конструира вектор диаграма на тока, приемайки, че моментните текущите стойности в първия и втория клонове зад напрежение съответно и (ris.152).
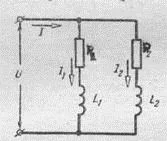
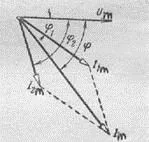
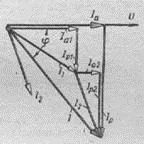
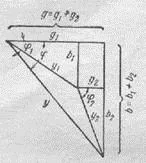
RIS.151 RIS.152 RIS.153 RIS.154
Амплитуда и сила на тока ефективни стойности на клоните могат да бъдат намерени с помощта на следното уравнение:
, , , , .
С помощта на векторна диаграма, и тези отношения, можем да намерим текущата стойност на мощността на тока и фазовото изместване между тока и напрежението:
,
Съответно, можем да изчислим активни, реактивни и очевидни клонове мощност ,,,
, , , както и активен, реактивен и активната мощност на цялата верига:
, , .
Ако един от клоновете да бъдат включени капацитивен товар, векторът сила на тока в този клон на вектора напрежение ще надмине определен ъгъл, и стойността на текущата сума и преминаването фаза ще се определя от съотношението на реактанс клонове.
Ако веригата на повече от две успоредни клонове, а след това на рационално изчисление се използва метод проводимост, която се основава на следното.
1) ток във всяка верига е вектор сумата от активни и реактивни компоненти (ris.153). Например, настоящите стойности за верига течения в клоновете обсъдени по-горе може да се изчисли по следната формула:
2) Активните съставки са във фаза с напрежението и равна :,
, , където g1 и g2- активно провеждане на първия и втория клоните.
3) реактивни компоненти на тока са различни във фаза от напрежението през и изчисляват както следва:
, , , , където В1 и В2 - реактивна проводимост първи и втори клонове.
Тогава :, където - общата проводимост на двата клона.
Проводимостта на цялата верига може да се изчисли по следната формула:
, където G = G1 + G2, и б = b1 + b2 и представени триъгълник проводимости (ris.154), което е вследствие на настоящата вектор диаграмата.
4) общият ток във веригата могат да бъдат проектирани като модул на вектор сумата от активни и реактивни компоненти, и къде.
5) Промяната на фазата между тока и напрежението или.
6) е активен, реактивната и пълната мощност на веригата може да се изчисли чрез формулите: ,,,
Като цяло, с разклонена верига използва метод, еквивалентен (еквивалент) вериги, т.е.. Е. Верига опростят последователно заместване на съпротивлението на разклонените части еквивалентни съпротивления. За тази изчислени активни и реактивни успоредни клонове проводникова и след това общата проводимост и съпротивление на разклонена част. В резултат на това с разклонена верига се заменя с прав - еквивалент. След това се изчислява ток, фаза смяна между тока и напрежението, активната, реактивната и пълната мощност верига.