√h Функцията у, неговите свойства и график

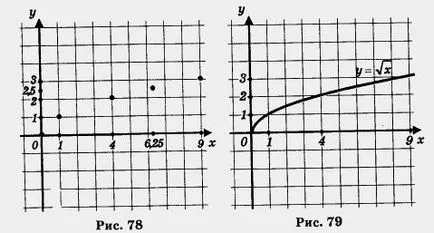
Построява точка резултати (0, 0), (1, 1), (4, 2), (6.25, 2.5), (0, 3) на координатна равнина (Фигура 78.). Те са разположени по линия, той съставя (фиг. 79). функции имат график. Забележка: Що се отнася до графика на ординатата в точката (0, 0). Имайте предвид, че, с модела на парабола у = х 2, лесно можете да го използвате, за изчертаване на функцията. защото тя е - клон на същата парабола, но не и насочени нагоре и в дясно.

свойства на функцията
Описването на свойствата на тази функция, ние имаме, както обикновено, ще разчита на неговата геометрична модел - клон на парабола (Фигура 79.).

1. Област на дефиницията на функцията - на рентгенова [0, + ∞).
2. у = 0 за х = 0; у> 0 за х> 0.
3. Функцията се увеличава с рентгенова [0, + ∞).
4. Функцията е ограничен от по-долу, но не ограничена от горе.
5. unaim. = 0 (получена при х = 0), не unai6 съществува.
6. Функцията е непрекъсната върху лъч [0, + оо).

Нека обърнем внимание на един любопитен факт. Да разгледаме две функции: у = (неговата диаграма е показана на Фигура 79.) и у = Х2, където х> 0 (неговата графика е показано на фиг 80.). Ние току-що изброените шест имоти за първата функция, но това абсолютно има същите свойства и втората функция. Разговор "портрети" на две различни функции на една и съща. Математика не можеше да понесе тази несправедливост, когато различните функции с различни графики. устно описва същото. Те откриват големи различия в естеството на графиките, отбелязвайки, че графиката на функцията е изпъкнала нагоре, докато
графика на функция у = х 2 където х> 0, изпъкналост обърната надолу.

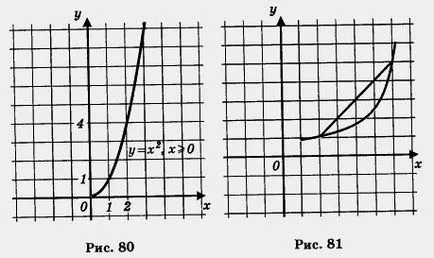
Тя обикновено се казва, че функцията е изпъкнала надолу, ако свързването на всеки две точки на прав сегмент на график, се установява, че съответната част на графика се извършва под сегмент (Фигура 81); на функция е изпъкнала ако, чрез свързване на всеки две точки на прав сегмент на график, се установява, че съответната част от графиката е над сегмента извършва (фиг. 82).

Изпъкналостта имот занапред ще включва графичен процедура четене.

функция у = F В (х), където е (х) =. Той приема всяка неотрицателна стойност. В действителност, без значение каква е ш специфична стойност> 0, или набор, винаги има х, така че F на равенство (х) = у, т.е. = Y; това е достатъчно, за да сложи х = у 2. Множеството от всички стойности на функцията обикновено се нарича домейн от функционални стойности. За функция у = стойности площ стойности лъч е [0, + ∞). Това, между другото, е добре чете на графиката на функцията (фиг. 79). Ако очаква графиката на у-ос, и просто обръщане на лъч [0, + ∞).

Пример 1. Виж минималните и максималните стойности на функция у = в сегмента:
а) [0, 4]; б) [1, 5].

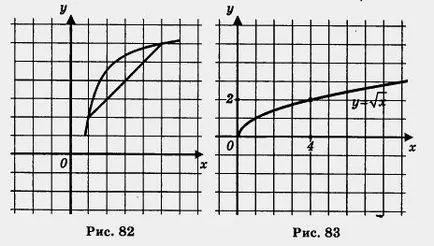
Разтвор) изграждане на графика на функция у = и изолиране на част от интервала [0, 4] (фиг. 83). Забелязваме, че Unaim. = 0 (получена при х = 0) и unai6 = 2 (постига, когато х = 4).

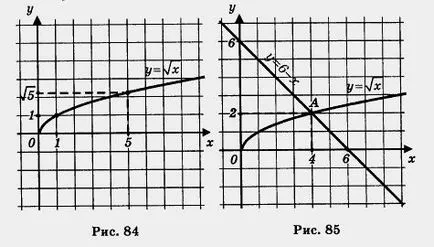
б) Построява функцията Y = част и изберете интервала [1, 5] (фиг. 84). Имайте предвид, че unaim = 1 (се постига, когато х = 1) и unaib = (постига, когато х = 5).
За т в е т а) unaim. = 0; unaib = 2; б) unaim. = 1; натъртване =

Пример 2: решаване на уравнение 6 = - х.
Решение.

1) разглежда две функция у = 6 - х и у =
2) конструиране на графика на функция у = (фиг. 85).
3) Построява у линейна функция = 6 - х.
Това - линия, която може да бъде изработена от две точки (0, 6) и (6, 0). Директен показано на същата фигура (Фиг. 85).
4) С чертеж установи, че графики се пресичат в една точка А (4; 2). Наистина ли е? Потвърждаване: двойка (4, 2) и удовлетворява уравнението и уравнението у = у = 6 - х.
Това означава, че точката (4, 2) всъщност е пресечната точка на диаграми. Предварително уравнение има един корен 4 - е абсцисата на точка А.
Отговор: 4.
Пример 3. функция Парцел
Решение. 1) се пристъпи към спомагателна координатна система с произход в точката (1 -2) (пунктирани линии х = 1 и Y = - 2 на фигура 86) ..

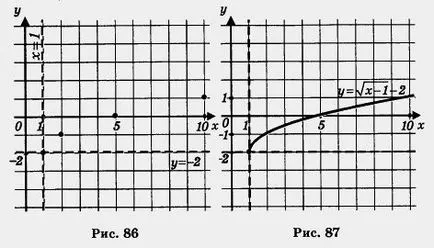
2) Равенство на функция Y = нова координатна система.
За да направите това, изберете контролни точки за = по функция у. например, (0, 0), (1, 1), (4, 2), (9, 3), но те няма да се изгради в старата и новата координатна система (тези точки са отбелязани на Фигура 86.). Построява клон на парабола, минаваща през избраната точка - това е желаният графика (Фигура 87.).

Пример 4. Конструкт и чете графика на у = -
Решение. Над в § 8, забелязахме, че графиката на функция у = - F (X) се получава от графиката на функция у = е (х) чрез превръщане на симетрия по отношение на оста х.
Използването на това, ние изграждане на графика на функция у = и карта симетрично спрямо оста х (фиг. 88). Това е графиката на у = -.

Ние списък на свойствата на функцията у = - (по график):
1. Област на дефиницията на функцията - на рентгенова [0, + ∞).
2. у = 0 за х = 0; при <0 при х> 0.

3. Функцията намалява по линията [0, + ∞).
4. Функцията е ограничена по-горе и по-долу, ограничена.
5 Unaib. = 0 (получена при х = 0), unaim не съществува.
6. Функцията е непрекъсната върху лъч [0, + OD).
7. Поле стойности на функцията - лъча (- OO, 0].
8. Функцията е изпъкнала надолу.

Пример 5. Конструкт и чете графика на у = е (х), където

Решение. Първо, ние изграждане на графика на функция у = разпределя част от него в интервала [0, 4] (фиг. 89). След конструиране на хипербола и изолиране на част от отворена лъч (4 + ∞) (фиг. 90). Накрая, двете "срезове", за да представляват по същия координатна система - това е графиката на у = е (х) (Фигура 91).
Ние списък на свойствата на функция у - F (х), т.е. Прочети графиката.

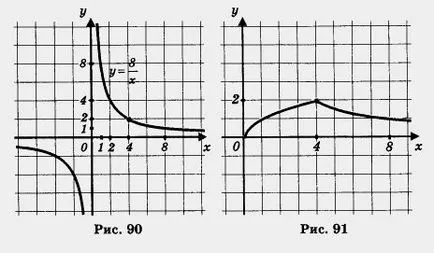
1. Област на дефиницията на функцията - на рентгенова [0, + ° о).
2. у = 0 за х = 0; у> 0 за х> 0.
3. Функцията издига в интервала [0, 4], и намалява по линията [4 + ∞).
4. Функцията е ограничен, и отгоре и отдолу.
5 Unaim. = 0 (получена при х = 0); unai6 = 2 (постига, когато х = 4).
6. Функцията е непрекъсната по предварително определен домейн.
7. Поле стойности на функцията - интервала [0, 2].
8. нагоре изпъкнала функция на интервала [0, 4], и е изпъкнал в посока надолу на лъча [4 + ∞).

Есета, домашна работа по математика за сваляне. учебници търкалят безплатни, онлайн уроци, въпроси и отговори

Ако имате корекции или предложения на този урок, моля свържете се с нас.

Ако искате да видите и другите корекции и предложения за уроци, погледнете тук - Образователен форум.