Знайте, Intuit, лекция, и координатите на векторите

Анотация: Основните математически понятия, свързани с определянето на позицията на обекта в самолета и в пространството, по своята ориентация и посока, както и техните обобщения за по-голям размер на пространството

Координати и вектори

Цифров ос нарича безкрайна права линия, които са определени: Точка O - произход; положителната посока на стрелката; измерване скала (номера на отлагане в принцип ос, често показва единица). Условно изображение на недвижими линия (CNC лъч) е показана на фиг. 3.1.

Фиг. 3.1. номер на ред

За се определя всеки реално число х върху реалната ос R само точка, съответстваща на неговия размер (представляваща броя с избрания размер и рамката) и обратно, тоест съвкупността от R и множество точки на реалната ос може да бъде свързан чрез една обща, еднозначно дефинирана правило право.

Пример. Броят 5 върху реалната ос съответства на точка отдалечена от мащаб разстояние е 5 единици от началната точка (еталонната точка 0).

Пример. А. дистанционно точка на разстояние от 3 единици от началото на скалата произход O за да сравните броя 3.

Брой линия намира обикновено в равнина хоризонтално на субекта, наречена ос X (Ox), редица линия намира обикновено вертикално към него, - оста Y (Oy) .Тези линии образуват система ориентация на всяка точка в равнината на двете координати.

В равнината, определена от две перпендикулярни (или, както казваме в областта на математиката, ортогонална) на номер линия, наречена хоризонтална равнина (XOY).

Всяка двойка от реални стойности (х; у) определя една точка М (х; у) в тази равнина, която се определя като точката на пресичане на перпендикулярни (ортогонални) линии, минаващи през стойности х Ox ос и стойността на у Oy ос. Обратно, всяка точка (х; у) може да се асоциира двойка реални числа: х - на Ox ос и Y - ос на Oy. По този начин определена система от две перпендикулярни линии наречените числен правоъгълна Декартова координатна система в равнината (фиг. 3.2).

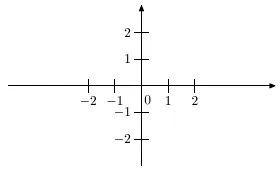
Фиг. 3.2. Декартова координатна система в самолета

Координатните оси обикновено са маркирани с букви.

Ox-ос се нарича оста х. ос Oy - ордината ос .Те ос XOY равнина се разделя на 4 части (координира ъгъл или, както те се наричат, квадранта).

Един подредени набор от три взаимно перпендикулярни оси с обща старт референтна точка (произход) и обща единица мярка за дължина (скалата) е Декартова координатна система в пространството .Oboznachaetsya такава система Oxyz или XYZ. Ox-ос се нарича оста х. Oy - оста у. Оз - на Z-ос.

Освен декартова координатна система често се използва и друго удобно, а не непременно правоъгълна координатна система.

Един от най-често използваните е полярна координатна система. определяне, както и в декартовата система, недвусмислена позиция на точката на самолета с два параметъра.

Да разгледаме точка на равнина O (наречена полюс) и простираща се от тази точка на половина (наречена полярен ос). Ако тази линия, за да настроите мащаба и положителната посока, а след това ние определяме полярна координатна система. Позицията на точка М в равнината, в полярната координатна система се определя от две числови стойности: - разстоянието м от точката на поле, т.е., и - ъгълът, образуван от сегмента ОМ и положителната посока на полярната ос. Ще означаваме точката с полярни координати във формата. Обикновено се смята, че. Тези стойности се наричат ​​основната стойност. Всяка точка на самолета е еднозначно определена от полярни координати. Изключение е само мястото, където ъгълът може да бъде произволно. Обикновено в този случай се взема от ъгъла.

Намираме връзката между координатите на точка М (х; у) в Декартова координатна система и нейните полярни координати в системата.

Построява се прав система XOY. където Ox ос съвпада с оста полярен, О (0, 0) - (. Фигура 3.3) произхода и положителната посока на тези оси съвпадат.

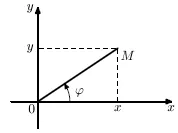
Фиг. 3.3. Polar и Декартова координатна система в равнината

Използването на правоъгълен триъгълник и тригонометрични функции, получаваме следните ключови съотношения:

По този начин, знаейки, точката на полярни координати, правоъгълни координати могат да намерят една и съща точка. Освен това, ако използваме основния тригонометрични съотношението и определението на допирателна училище разбира се (да се прибират площади х у у тогава разделени на х ..), следните зависимости са валидни:

По този начин, ако знаем правоъгълните координатите на точката, ние можем да се определят подходящите полярни декартови координати.

Пример. Ако след това се получава съответната формула

От това можем да извлече системата: у = х. х 2 + Y 2 = 16 или по-малко.

Пример. Уравнението на окръжност с център на произход и радиус R на в Декартова координатна система, както е известно, има формата: 2 х + у 2 г = 2. кръг уравнение в полярни координати е от формата

Така че, уравнението е много по-лесно в съзнанието :. В допълнение, това уравнение се освобождава от "излишния" параметър, който в този случай се счита, че някои от видовете. Работа с обекти в полярна координатна система често е по-лесно на практика, геодезични и др астрономията.

Удобен координатна система в пространството и е така наречената сферична координатна система. В тази система, позицията на точка М (х; у; Z) в пространството е еднозначно определена от разстоянието г от произхода (ОМ дължина сегмент), ъгълът между OM и положителния половин ос Оз и ъгъла (между ОМ проекция на XOY равнина и положителния половината оста Ox ( Фиг. 3.4).

Нека да се определи формата на комуникация сферична и декартови координати. Съгласно фиг. 3.4:

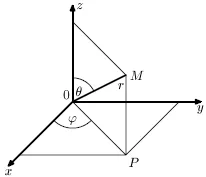
Фиг. 3.4. сферична координатна система