взаимодействието на въртене орбита (COS)
SOV- частици взаимодействие, при което количеството на взаимодействие зависи от стойността и разположението на завъртането и орбитална ъглов момент на частиците. Най-ясно изразени в атомите един електрон (водород и водородни-частици) и също така те включват алкални метали, тъй като в техните затворени обвивки Ll = 0, и следователно ъглов момент на атомите се определя само от стойността на валентността електронен импулс на. В случай на един електрон атом SOC представлява взаимодействието между електрон спин и магнитното поле, което се създава от орбитално движение на електрона. Ние очакваме, енергията на SOC в един електрон атом. Ние считаме, че движението на електроните в един атом в координатната система, свързана с електрон. В този случай, на електрона не е в движение и може да се предположи, че ядрото около електрона се движи по кръгова орбита със скорост, равна на скоростта на движение на електрони по отношение на ядрото на.
При завъртане на сърцевината еквивалент ток възниква по орбитата Iekv = Зе / T = Zev / 2πr, където
R- радиуса на орбитата
v- скорост на въртене електрон орбита
След ц = I · πr² = zevπr² / 2πr = Zevr / 2
ц = (| д | / 2 м) Z
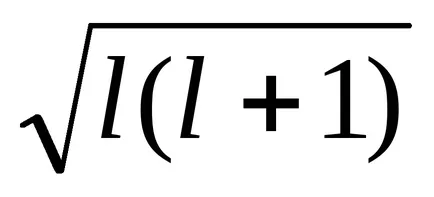
Приравняването на тези изрази, можем да извлечем израз на орбиталната скорост
За електрон о = Z
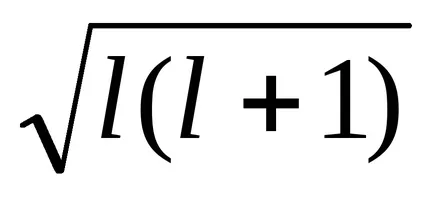
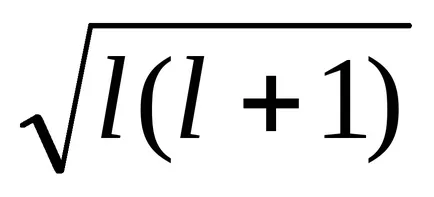
След това се обърна кръгови ток Ii трябва да се научим на индукция в центъра на кръгла ток, т.е. на мястото на електрона. Според Био-Савар-Лаплас:
В = μI / 2г = Зе ал
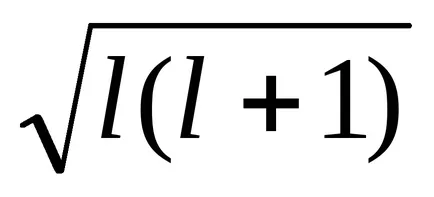
тъй като | д | ž / 2м = μB; B = zμ0 μB
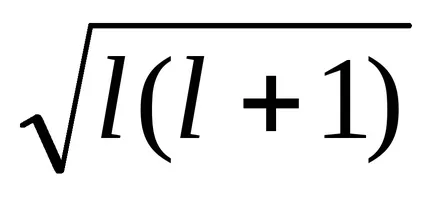
Енергията на взаимодействие на магнитния момент и на магнитното поле:
След това: ΔEsl = -μl · В = - (eЋ / 2М)
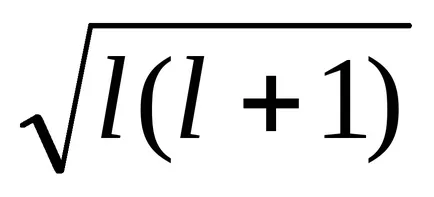
ΔEsl = -zμ0 μB
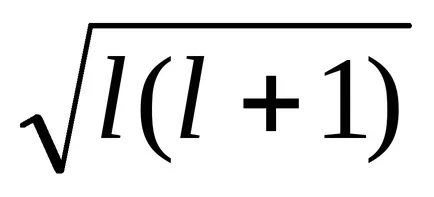
Радиус R = A / Z, тогава ΔEsl = -Z 4 μ0 μB

От този израз може да се види, че енергийните взаимодействие електрони S-Pril = 0 и следователно urovnis електрони са синглет. Dlyap, г и т.н. електронна енергия взаимодействие винаги се две стойности: ± ΔEsl, така че нивата на тези електрони с две стойности са дублети и това води до факта, че спектралната линия от водород и алкални метали също са дублети. На 2, 3 и т.н. електронни системи Данните за присъствието на картината е много по-сложно и води до разделяне на енергийните нива на голям брой компоненти. Разделяне на енергийните нива и спектралните линии поради SOC в атоми наречен фина структура на спектри.
На теория, водороден атом, който не се счита присъствието на въртене енергия се определя само от главно квантово число, присъствие води до същото завъртане SOC, при което енергията на атома става зависи и от орбитално квантово число L.
В един електрон атом. Добавяне на ъгловия момент на векторите в квантовата механика. Общият ъглов момент на електрона в атом. Вътрешен квантово число на електрона.
Състоянието на електрон в един електрон атом се характеризира с:
1) Ll - орбитален ъглов момент на електрона, абсолютната стойност е квантувани и е равна на |

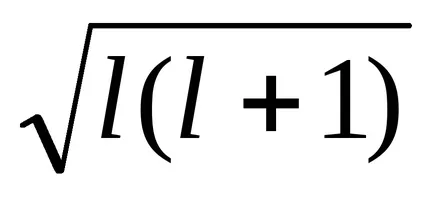
където мл - орбитален магнитно квантово число prichomml = 0; ± 1; ± 2; ...; ± л, NML = 2л + 1.
2) електрон спин също се характеризира със свой собствен ъглов момент Ls = Z

където MS - завъртане квантовата броя на магнитното, MS = ± 1/2.
В резултат на SOC се образува в резултат на което атом (пълно) ъглов момент |

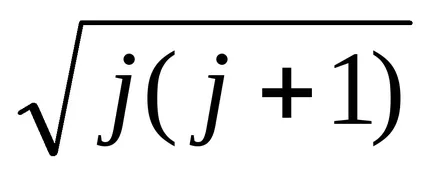
j-, където завършва (вътрешно) квантово число, и проекцията на общото момента от избраната посока: Ljz = MJ ž
-complete квантово число MJ и електрон на атом е оформен едновременно общата магнитен момент μj. SOC води до добавяне на квантовата вектори

Да приемем, добавя две квантовата вектор



|




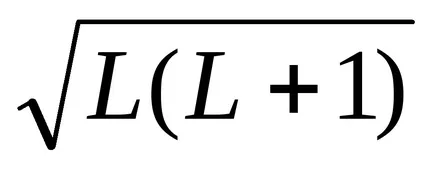
Освен векторите също добавят техните проекции на предпочитаната посока:
От това следва, че максималната стойност на издатъците, сгъване вектори съответно: L1zmax = Ћl1, L2zmax = Ћl2; LLzmax = ЋL защото проекция представлява Scalars, така проекцията на Полученият вектор е алгебрични сумата от гледна точка на вектори, полученият проекция ще бъде максимум ако проекцията на събираеми вектори имат същата посока:
От друга страна, проекцията на получения вектор ще бъде минимална, ако сгъваеми прожекционни вектори са противоположни посоки:
по този начин чрез прибавяне на Спектър на вектори съгласно ориентация може да се следните стойности:
По този начин тя може да се разглежда че добавянето на квантовата вектори намалени добавянето на квантово число, сгъваемите вектори не могат да бъдат ориентирани произволно. Ние намираме броя на ориентации сгъваеми вектори
L1 = Z
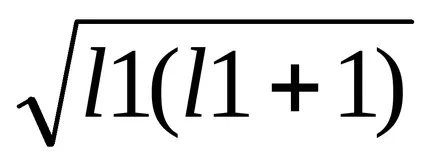
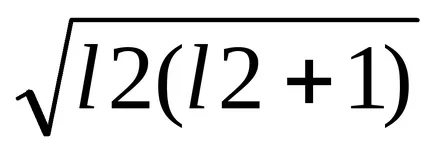
Резултатът:
LL = Z

Очевидно е, че ако l1 Вектор диаграма. Поставянето два вектора L1 = Z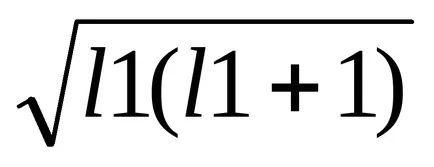

защото L2 Т.е. имаме 3 възможни ориентации сгъваеми вектори и получената квантовата броя lbudet бъде в otl1 + L2 = 3 и | l1 -L2 | = 1 Следователно стойността на получения вектор L ^