Връзката между графиката на функцията и графиката на негово производно - решаването на проблемите на контрол

Връзката между графиката на функцията и графиката на негово производно

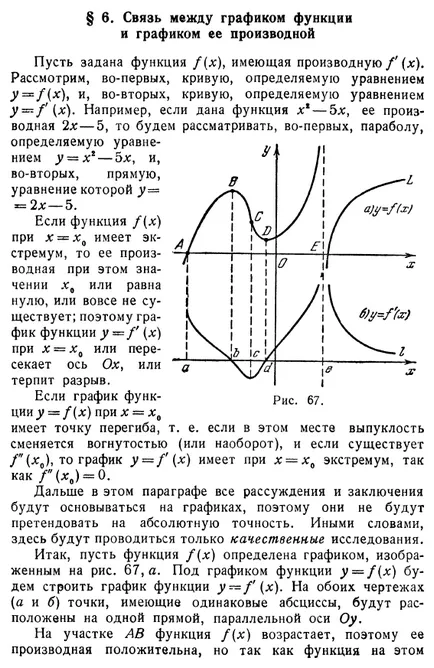
Връзката между графиката на функцията и графиката на негово производно Нека функция е (х)> като производно / '(х). Помислете, първо, кривата, определена от уравнението у

/ (X), и от друга страна, кривата определя от уравнението у = ZF (х). Например, ако дадена функция х * - 5ls, негово производно 2-5, тогава ще прецени, първо, параболата определя от уравнението у - х - о, и, второ, по права линия, чиито уравнение е у = == 2 - 5. Ако функция / (X) при х = x0 има екстремум, негово производно при тази стойност x0 или равно на нула, или не съществува; Следователно графиката на у - е (х) при х = x0 или х-ос пресича или прекъсване. Ако графиката от фиг G7 ЛИЗАЦИЯ функция у = е (х) при х = x0 е точка на инфлексия, тоест, ако в този момент заменя изпъкналост вдлъбнатина (или обратното), и има F "(x0), след това графиката на у .. - е '

4) "8 (* + 2)" 3 3 и в § 3, глава III се конструира hsh- парабола Y ^ = Arg; leg- 03 мар да се види, че функция х CH е производно на (х-1x4-2) на функция V-V>. Ако се съчетаят тези графични функции на ции, ние получаваме на снимката е показано на фиг. 68. Тази фигура потвърждава по-горе. Упражнения към глава. VIII 1. Виж критичните стойности и изследват за намаляването и увеличаването на XM функция у = -16 х. 2. Виж критичните стойности и изследват за увеличаване и намаляване функция # = X9 + ^ -х * + U 3. Виж критичните стойности на функция у - е *. 4. Намерете най-критичните стойности на функцията