Вектори в космоса
Декартова координатна система.
Директни X, Y, Z координатни оси се наричат (или координатните оси),
тяхната пресечна точка О - произход,
и XOY равнина. xOz и yOz - координатната равнина. О точка разделя всеки координатна ос на две половини линии, които се наричат положителните и отрицателните полуремаркета оси.
Координата на точка А на оста х се нарича номер равен на абсолютната стойност на OAx дължина сегмент. положително, ако точка А се намира на положителен половината х. и отрицателен, ако тя се намира на отрицателна реална ос. По същия начин, може да се определи координатите Y и Z координатите на точка А. е писано в скоби до името на тази точка: А (х; у; Z).
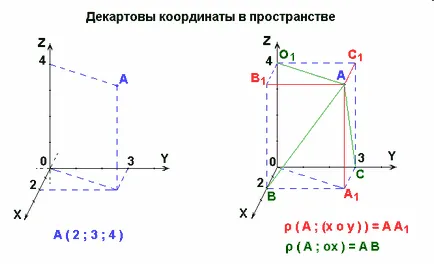
Един вектор или единичен вектор е вектор, чиято дължина е равна на една и който е насочен по продължение на ос координира. Vector аз. к. к е координатната вектори. Всеки вектор може да се разгражда от координатните вектори: коефициенти на разширение са определени еднозначно и нарича координатите на вектора в тази координатна система.
- вектор единица по оста х. означен с т. - А единичен вектор насочена по оста у, е обозначен с к. - вектор единица по Z-оста е обозначен с к.

Ø Координати нулев вектор е нула.
Ø Координати равни вектори са равни.
О, координатите на вектор сумата от два вектора е равна на сумата на съответните координати на тези вектори.
Ø координати на вектор разликата на два вектора е равна на разликата на съответните координати на тези вектори.
Ø вектор координати на вектор продукта от броя равна на произведението на съответните координати на вектора за този номер.
IV. Консолидиране. (Мултимедийна презентация) Решение относно завършени задачи за рисуване
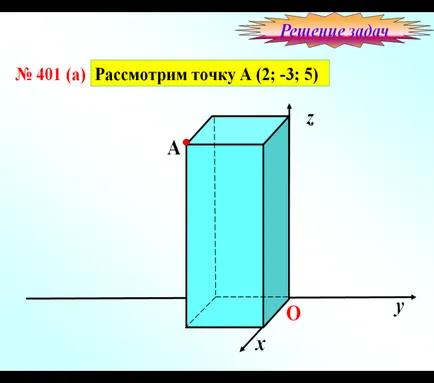
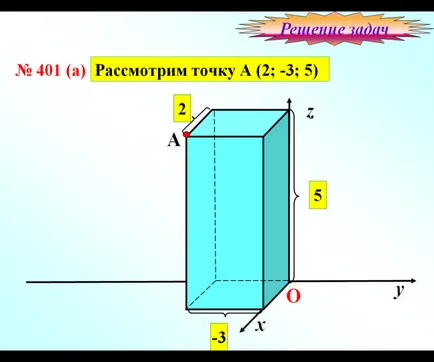
Задача №1 Помислете точка А и да намерят своите координати в чертежа: A: A (2; -3; 5)