Вектори и скалари - studopediya
Стойностите за задачата, която само едно число, наречени скаларна. Примери за Scalars могат да служат като път, маса, време и т. D.
Стойностите за работа, които изискват числова стойност и посока, наречени вектори. Примери за вектори са, например, преместване, скорост, ускорение, сила и така нататък. Г. Векторите могат да бъдат определени с един букви стрелки (,.,). При липса на стрелка означава същата буква или стойност modulsootvetstvuyuschego вектор цифров. По този начин, вектор единица.
вектор модул - скаларна, което винаги е положителен. Показано на фиг. 1а P. вектор допълнение операция символично писмено, както следва:
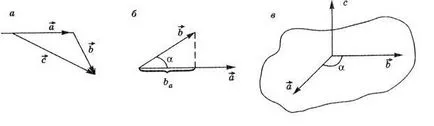
В резултат на умножение на вектор от скаларна и резултатът е нов вектор, modulkotorogo с фактор повече от вектор и посока съвпада с посоката на вектора ако скаларни е положителен, и противоположно на това, ако скаларни е отрицателен.
продукт точка на два вектора, и - това е количество скаларна равна на произведението на вектори и модули, умножена по косинус на ъгъла между тях;
където във формула въведен вектор проекцията върху вектор посока (б = б защото # 945) (. Фиг A.1b).
Вектор продукт, и - това е вектор равни по абсолютна стойност на продукта на векторите на модули и синуса на ъгъла # 945; между тях (фиг. P.1v).
Вектор е перпендикулярна на равнината, в която могат да бъдат намерени на векторите и неговата посока, например, съгласно правилото за правило дясната - въртеливото движение на палеца трябва да съвпада с посоката на най-късата включване на, след това си движение напред дава посока.
2. Градиент скаларна velichinya. В пространството някак разпределени скаларно количество и - тя може да бъде поле температура (а = T), потенциалната енергия (а = U) и т.н. Такова поле може да се характеризира като градиент ... Под градиент количеството вектор скаларна разбере, че всяка точка в пространството е насочено към най-бързото нарастване и числено равно на стойността на нарастване на единица дължина в тази посока.
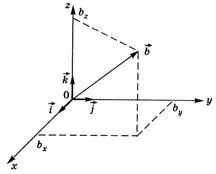
При изчисляването на производно стойността на координата х в формула (A.4) се счита, че координатите Y и Z остава постоянна - това производно се нарича частично производно заедно х координира:
Подобни предположения се приемат в изчисляването на частични производни по отношение на координатите Y и Z.
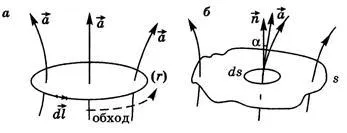
Вземи в неравномерно поле въображаем затворен контур Г. Определяне на произволна посока на прекосява и въвеждане на вектора равна на дължината модул на елементарни dlkontura. Във всяка точка на вектора съвпада с допирателната към контура и се отнася по байпас верига (Фиг. P.3a).
След това движението на вектора в произволна затворен контур R се нарича интеграл от следния вид:
Може да се твърди, че ако движението на вектор вектор поле по произволен затворена пътека Т е нула, тогава тази област е потенциал (например, електростатично поле вектор). Ако движението е над произволно затворен контур R е различно от нула, тогава полето вектор не е потенциал, то се нарича поле вихър.
Ние се въведе понятието поток F вектор. Вземете в неравномерно поле вектор на произволна повърхност S. изолира елементарни й DS площ и въвеждане на вектора насочена по вектора перпендикулярна на повърхността (фиг. P.3b). Модулът е квадратни повърхностен елемент DS.
Тогава DF вектор елементарен поток се нарича стойност DS cherezploschadku на
Обобщавайки DF протича през тампон повърхност DS S. намери вектор поток през повърхността S:
Ако приемем, че модулът на вектор плътност определя областта на вектор в даден момент, тогава вектор поток е числено равно на броя N на линии, проникваща повърхността S.
4. Различие и ротора на векторна .За решаване на практически проблеми е необходимо да се прилагат математическия апарат, който позволява да се разгледа вида на векторни полета, не само в голям обем на пространството, но също така и в малък квартал на една точка. За тази цел ще се въведе концепцията на отклонение () и ротор () вектор.
Обърнете поле V. обем ограничена от затворената повърхност S. и ще styagivatpoverhnost в малък съседство на точка А (фиг. P.4a)
Тогава различието на вектора е границата
За отклонение се характеризира с наличието на източници на първия тип в малък съседство на точка А, например, електрически заряди (фиг P.5a.):
където # 961; - плътността на заряда.
В математиката, за да можем да напише следния израз: