Условно (относително) екстремум

§ 8.19. Условно (относително) екстремум

В клавиша за интервал. От геометрична гледна точка, тази функция представлява квадрата на разстоянието от началната точка на правоъгълната координатна система. Това не е най-високата стойност инча Но ако това се счита само за точки на елипсата, то е ясно, че тя достига максималната си стойност в точките (фиг. 101).

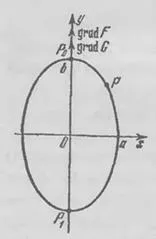
Така, функцията, разгледани в цялата равнина, има най-голяма стойност, но същата функция е предвидено, че се намира на елипсата, има най-голямата стойност (два пъти).

Тази ситуация ни води до проблема за намиране на екстремум на функцията при условие, че аргументите си да отговарят на някои допълнителни ограничения. Така че, нека се има предвид функцията

променливите. Задължително да намерите екстремум на функцията при условие, че променливите са свързани с

обикновено се нарича уравнения ограничаващите.

Системата от уравнения (1) определя пространството, най-общо казано, набор, което ние наричаме повърхността.

О N ° С д и д п д. Ние се каже, че една точка, отговаряща на уравненията (1), е местно условно (относително) максимум (минимум), ако точка съседство, така че този квартал отговарят уравнение ограничение (1), следното неравенство

Точка местната условно максимална или минимална точка се нарича условно местно (относително) екстремум.

В горния пример това е точка условно локален максимум, тъй като всички точки, лежащи на елипсата.

Нека първо се изясни въпросът за необходимите условия, за да точката е относителната точка на местна екстремум. Да - точка ограничени оптимизация и функции са непрекъснати частни производни и Jacobian

в квартал на тази точка.

Както е известно, на системата (1) може да се преобразува по отношение на променливи в квартал на:

където функциите имат непрекъснати производни на мястото.

Заместването на тези функции, ние откриваме, че е функция само на променливите независими една от друга:

Очевидно е, че ако условно достига местен пункт за екстремум, а след това тя достига в нормален местната точка за екстремум, или, както каза абсолютна местно екстремум, както и обратното.

Но след това, както знаем, равенства

където - диференциалите на независимите променливи.

Точка за които с оглед на (1) (или (3)) притежават (4) ще се нарича неподвижна точка на присъствието на връзки (1).

Ние сме доказали, че точка е точка на местно ограничени оптимизация, е необходимо, че е неподвижна точка в присъствието на връзки (1).

Нашата по-нататъшно разглеждане, свързана с въпроса за това как да намерите определена фиксирана точка, не позволява на системата (1) по отношение на променливите, въпреки наличието на функциите приемем. Пишем заедно.

По силата на инвариантност на формата на първата разлика за състоянието (4) е равна на:

където членовете на зависимите разликите са равни

Тези диференциали с независими диференциали са свързани с

че ние получаваме от уравнения ограничаващите.

По този начин, неподвижна точка на присъствието на връзки (1) може да се определи, както и точка, отговаряща на уравненията (1), че следното уравнение (5) за всички, за които равенства (6) за него.

Представяме - мерни вектори

На езика на тези вектори на уравнение (5) и (6) могат да бъдат написани по отношение на скаларен продукт на

Стигнахме до една точка е неподвижен точка в присъствието на линкове (1), ако и само ако отговаря на уравнението (1), и ако е фактът, че вектор е ортогонален на наклона, от това следва, че е ортогонален. Но в този случай (обяснение по-долу) съществува уникална система от числа, така че

Обратното също е вярно. Ако е известно, че при определени номера могат да бъдат представени под формата (7), т.е.. E. като линейна комбинация от градиенти, следва веднага, че след като вектор, перпендикулярна на градиентите ортогонални автоматично.

Уверете се, лоялност към обратния твърдението, че няма проблем: (7) и (6 '), че

Що се отнася до твърдението, ние се позоваваме на една теорема на линейна алгебра. Всеки от нас направи обяснение.

Да предположим, че линейно подпространство калибрира от векторите R. Е. Комплект от линейни комбинации на формата (7), съответстващи на всички възможни номера система. Ние въведе подпространството на вектори ортогонални, т. Е. Състои се от всички вектори ортогонални или, еквивалентно, ортогонални вектори. Ако ортогонален, а след това, обратно на ортогонална, т.е.. Е. Състои се от всички вектори взаимно перпендикулярни. Както бе споменато в стационарна точка на градиента е перпендикулярна на всички вектори, ортогонални градиентите, т.е.. Д. е перпендикулярна на градиента. Тогава от теорема споменатият градиент принадлежи, така че е линейна комбинация на градиентите уникален линейна комбинация, защото градиентите образуват линейно независима система. Фактът, че матрицата на частични производни на функции

Той се намира в близост до ранг, защото ние приехме, най-добро състояние (2), но след това редовете на тази матрица определят вектори (наклони) образуване на линейно независима система.

От гореизложеното следва, че фиксираната точка на функцията в присъствието на връзки (1) може да се определи така: това е точка, отговаряща на уравнението (1), за които градиента е линейна комбинация на градиентите

Можем също така да кажа това: да се посочи

е определена за функция с връзки (1), че е необходимо и достатъчно, че съществуват цифрите за нея, за които равенството (7).

Тъй ранга на матрицата (8) в точка, равна на всяка неподвижна точка съответства на уникална система номера, които удовлетворяват уравнение (7). Уравнение (7) е равен на:

Функция под знака на градиент в (9)

наречен Лагранж, а броят на Лагранж множители.

Пишем условията (9) в разгънато състояние:

Проблемът за намиране на присъствието на стационарни точки връзки (1) намалява към разтвора на системата, състояща се от уравнения (1) и.

За да намерите стационарна точка

функция в присъствието на отношения, е необходимо да се направи функция Lagrange и системата от уравнения (9 ') и решаване на тази система във връзка с ограничение уравнение (1). Общо ще уравнения там с неизвестни. В тази система, както и да се произнесе по този въпрос, което е неподвижно точка. Местните екстремум точки са сред условни стационарни точки. Да се ​​изясни въпросът дали това всъщност би неподвижна точка точка ограничени оптимизация, се провежда чрез третиране на втората разлика на Лагранж. В изясняване на знака трябва да се счита, че тези различия и зависят от диференциалите.

ПРИМЕР Пример. Нека самолет даден фигурата, ограничена от координатните оси и парабола. Fit който е в тази фигура правоъгълник със страни, успоредни на координатните оси, един от върховете на тази парабола, така че площта на правоъгълника е най-голяма (фиг. 102).

R е с т н д Нека ф -. Vertex координати. Тогава площта на правоъгълника. Освен това, тъй като на мястото се намира на параболата, тогава нейните координати, трябва да отговарят на уравнението на параболата. Ето защо, ние трябва да проучи условен екстремум на функцията в присъствието на комуникация. Функцията на Лагранж. Намираме се стационарните точки на задачите на уравненията

Решаването на тази система, ние откриваме, че. По този начин. Фиксирана точка и тя отговаря на множителя на Лагранж. Проверяваме неподвижна точка на втория диференциал Лагранж

където през последните два мандата от дясната страна там, защото диференциали и независим и най-общо казано. Въпреки това, в неподвижна точка.

Ако приемем, и диференциалите на независимите променливи, тя не е сигурен знак. Въпреки това, от ограничението уравнения може да се види, че на мястото. По този начин,

и, следователно, на нарастване на функцията на мястото, съответстващо на стъпките е по-малка от нула (). Следователно, функцията е в местната условно максимум.

Така че, на всички правоъгълници горе формират най-голямата площ на правоъгълник със страни.