удивителен баланс

Има много различни дизайни и конструкции, въпреки, че човек се чуди как те пази равновесие. Може би най-известният от тях - най-известния Наклонената кула, построена през 1360 и запазва своята неволно наклон. Защо кулата в Пиза пази равновесие? Тайната е проста. Вертикалната проекция на центъра на тежестта на кулата е въз основа на нея. Това е вярно за всички други съоръжения. Също така, ако даден обект, за да виси над точката, която съвпада с центъра на масата, на окачен елемент също ще се запази балансът. Можете също така да събира предмети от различни дизайни най-странните форми, които ще бъдат в равновесие, ако правилно изчисляване на местоположението на центъра на тежестта. Нека се опитаме да разберем как да се изчисли координатите на центъра на масите на различните равнинни фигури.

Да предположим, че сте решили да направите коледни гирлянди, състоящ се от най-различни форми, включително и под формата на стрела. Първо трябва да се изрежат на строителство хартия с Нова година изготвянето равнобедрен триъгълник. След това трябва да се направи разреза, също във формата на равнобедрен триъгълник, така че центърът на тежестта на получената цифра се появи на точка Б (виж фигурата). Намираме координатите х и у в в центъра на масата на фигурата в правоъгълна координатна система yOx.

Позицията на центъра на тежестта на равнинни фигури честота: центъра на масата на триъгълника е в пресечната точка на неговите медианите на масовия център на правоъгълника е в точката на пресичане на диагоналите, масовото центъра на кръга съвпада с центъра. Тъй като триъгълник ACD - равнобедрен, след това, като се излиза от неговия симетрия по отношение на правата линия ОА. От това следва, че х С = 0.

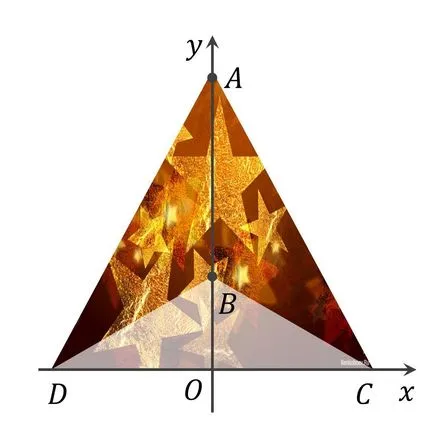
За изчисляване на координатите у С използват следната формула:

Като се има предвид, че центърът на тежестта трябва да бъде в точка Б. получите:

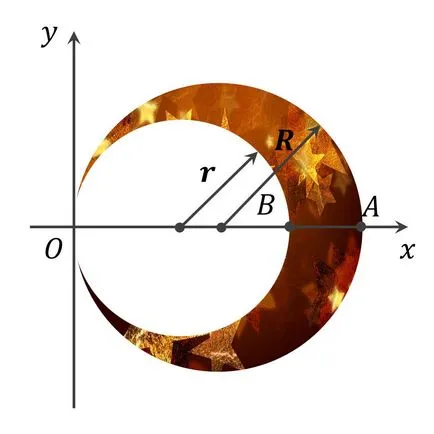
Според предложения метод, ние Ви предлагаме да се реши проблема:

Изчислява центъра на масата координати на окръжност с радиус R със срез окръжност с радиус R (вж. Фигура). Определя какво трябва да бъде съотношението на радиуса R и R. че центъра на тежестта на фигурата е в точка В. Анализ на резултатите.