траектория, дължина на пътя, изместване вектор

Преместването с течение на времето от една точка до друга, тялото (материална точка) описва някои линия, която се нарича траекторията на движение на тялото.

Има пет движения на твърдо тяло, и съответно пет вида траектории:

• Постъпателно движение на тялото в кинематиката, съответстващи праволинейно движение на точка;
• Това съответства на въртеливото движение на движение на тялото на точка на обиколката;
• плосък движение тяло съответства на движение на точка на самолета;
• сферична движение тяло съответства на движение на точка върху повърхността на сфера;
• свободното движение на тялото съответства на движението на точка от произволна траектория.

Определяне на положението на точката от координати х = х (Т), у = Y (т) и Z = Z (т) и радиус вектор $ \ overrightarrow \ наляво (т \ дясно) $. $ \ Overrightarrow $ - радиус вектор позиция на точката, в началното време

Законът за движение определяне на позицията на материална точка в пространството по всяко време може да се определи или координира начин, през време зависимостта на координатите х = х (Т), у = Y (т), Z = Z (т), или метод вектор, през време на зависимостта радиус вектор $ на \ overrightarrow = \ overrightarrow \ наляво (т \ дясно) $, от произхода на дадена точка (фиг. 1.1).

Преместването на тялото $ \ overrightarrow = \ триъгълник \ overrightarrow> = \ overrightarrow- \ overrightarrow $ нарича посока на отсечката, свързваща началната и крайната точка на traetktorii на тялото. L е изминатото разстояние дължината на пътя, изминат от тялото през време тон.

Изминато разстояние $ л $ и изместване вектор $ \ $ overrightarrow най движение krivolineynom тяло. $ A $ и $ б $ - началната и крайната точка на пътя

Както се вижда от фигура 2, движението на тялото в обем вектор извит път единица е винаги по-малко изминатото разстояние.

Преместване - вектор количество. Това насочено сегмент.

Path - скаларна величина. Този номер.

Сумата от две последователни движения от точка 1, точка 2 и от точка 2 до точка 3 се движи от точка 1, точка 3 (Фигура 3.):

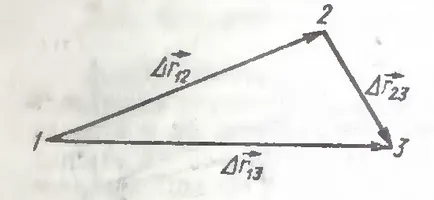
Фигура 3. Размер на две последователни движения.

Ако по време на радиус вектора на материална точка Т е $ \ overrightarrow $ (Т), и по време на $ т + \ триъгълник т $ е $ \ overrightarrow $ (т $ + \ триъгълник $ т). след това се движат $ \ триъгълник \ overrightarrow $ по време на интервал от време $ \ триъгълник т $ сума: $ \ триъгълник \ overrightarrow = \ overrightarrow $ (т $ + \ триъгълник т) - \ overrightarrow $ (т)

Преместването $ \ триъгълник \ overrightarrow $ има функция на времето т: $ \ триъгълник \ overrightarrow = триъгълник \ overrightarrow \ (т) $