Теорема на баланса на силите и метода на разлагане на силите на компоненти

теоретична механика

Теорема на равновесие на системата за равнина на три неуспоредни сили

Теорема на равновесие на системата за равнина на три неуспоредни сили могат да бъдат формулирани както следва: е необходимо, но не достатъчно на линията на действие на тези сили на равновесието на системата за равнина на три неуспоредни сили се пресичат в една точка.
Нека се опитаме да докажем това твърдение, както и да обясни защо на условията, предвидени в теоремата не е достатъчно за баланса на силите система.

Да предположим, че три сили P. Q и F лежат в една равнина, линията на действие на сили Р и Q се пресичат в точка А.
Въз основа на изследването на III и IV аксиоми статичен трансфер Р сили и Q заедно линии на действие точка А. Въз основа на паралелограм аксиома намери получената от тези сили FΣ.
В резултат на това получаваме система от две сили - FΣ и F., която е еквивалентна на първоначалната система на три сили.
Но, според Аксиома III на, баланс е възможно само ако FΣ на сили и F лежат на една и съща права линия и насочено в противоположни посоки, което означава, че линията на действие на сила F. принадлежност към оригиналната система на три сили, също трябва да премине през точка А ,
Това доказва теоремата.

Тази теорема показва само, когато е необходимо състояние на равновесие, което не е достатъчно, тъй като трите сили могат да се събират в една точка, но не са в равновесие, ако тяхната векторна сума не е нула.

линии на действие на силите, които се пресичат в една точка, наречени са сходни.

Разлагане на сила на два компонента

Разлага на учредително власт - е да се намери система сили, се равнява на силата. Като цяло, разлагането на задача сила на два компонента има безкраен брой решения, като силата - вектор размер.

За да направите задачата трябваше окончателно решение, трябва да се определят две условия, като например направления или модули два компонента. Има четири възможности FΣ разширяване сила на два компонента P и Q. прилага в същата точка. Във всички случаи, решението се свежда до изграждането на успоредник на силите.

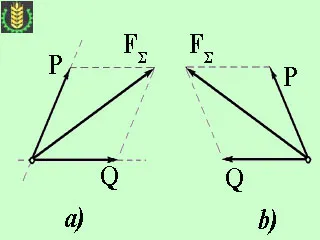
1. Има области на два компонента Р и Q (Фигура а).
В този случай, предварително определена посока на Р сили и Q от точката на прилагане на сила FΣ. тогава ние построи успоредник на силите, като вектор FΣ сила на диагонала на успоредника.

2. известен големината и посоката на един от компонентите.
Разтвор графичен метод, както в първия случай се редуцира до изграждането на успоредник; където известен големината и посоката на една от страните и диагоналите на успоредник (Фигура б).

3. Известни модули два компонента Р и Q (посока не е известно).
Проблемът е решен с жлебовете, при което челюстите на началото на вектора на сила FΣ провежда дъга радиус равен по модул компонент (Р или Q) от двете страни FΣ вектор. след това от края на вектора проведе FΣ дъга радиус на втория компонент от двете страни FΣ вектор. дъги пресичащи точки са върховете на паралелограм на силите желаните.
Проблемът в този случай могат да бъдат:

4. Известен компонент посока и Q компонент на второто устройство P. Проблемът се решава чрез сериф метода. Така от началото на вектора се извършва FΣ форма линия в посока на вектор компонента на силата, и след това до края на вектора се извършва FΣ линия, успоредна на първия ред. Освен това, от началото на втория вектор FΣ линия направена серифи дъга, чийто радиус е равен на втория модул, известен компонент.
Задачата може да бъде:

• едно решение, ако разстоянието между успоредните линии конструирана равна на дължината на компонент на сила образуват модул (в този случай ъгълът между вектори Р и Q е равно на 90 градуса);
• две решения, ако разстоянието между успоредните линии е по-малко от дължината на известен компонент на модула за сила;
• не на решения, ако разстоянието между успоредните линии е по-голяма от сила компонент известен модул.