таблични интеграли

§4.3 Прекият интеграция, интеграция чрез заместване, интеграцията на части

Интеграцията се нарича пряко, само ако свойствата на интеграли и таблични интеграли се използват в процеса на интеграция.

@ 1. Цел Интегриране функция

.

Решение: Интегралът се изчислява директно използване на свойствата на неопределени интеграли и интеграли маса:

Забележка. Не е необходимо да се напише за междинни изчисления за всяка интегрална постоянното му план; достатъчно, за да го приписват да извърши всички интеграции.

Този метод се използва, като правило, ако подинтегрален е трудно и не може просто да вземе интеграл чрез таблица на интеграли.

В подинтегрален се въвежда вместо х спомагателни променлива Z. свързани с х зависимостта на (обикновено сложна функция аргумент подинтегрален), след това намалява до интеграла табличен неразделна.

@ Проблем 2. Изчисли.

Решение: Замяна на променливи 2х - 1 = Z, тогава 2х - 1 = Z и DX = DZ / 2 са заместени в подинтегрален и интеграл се редуцира до табличен интеграл:

.

@ Проблем 3. Изчисли.

Решение: Замяна на променливи 1 + х 2 = Z, след това се намери 2xdx = DZ. След заместване получаваме:

.

@ Проблем 4. Изчисли

.

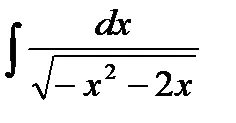
Решение: В рамките на корен квадратен, като подчерта перфектен квадрат, интеграл може да бъде намалена до табличен интеграл:

.