Свойства на детерминантите на матрици
Нека да формулира основните свойства на детерминанти, присъщи детерминанти на всички поръчки. Някои от тези свойства, за да обясни на определящите фактори за третия ред.
1. Ако някой ред (колона) матрица се състои от всички нули, след това си детерминанта е 0.
2. Ако всички елементи на всеки ред (колона) на матрицата се умножават по редица. След това му детерминанта се умножава с този номер.
Доказателство. Нека определящ фактор за оригиналната матрица е. За определяне на първия ред на матрицата размножават на. Има нов фактор. които се разшири върху елементите на първия ред:
За определящ общ фактор може да направи всеки ред или колона, за разлика от матрицата като знак, който може да бъде взето само общ фактор на всички елементи.
3. При преместване на два реда (колони) на детерминанта на промените на матрицата на обратен знак.
4. Ако матрицата съдържа две идентични ред (колона), тогава детерминанта е нула.
Доказателство. Наистина, пренареждане на редовете (колони). От една страна, определителят не се променя, но, от друга страна, от имота 3 промени подписват, т.е. , къде.
5. Ако елементите на двата реда (колони) на матрицата са пропорционални, нейната детерминанта е нула.
Доказателство. Да предположим, че за определеност, които са пропорционални на първия и втория ред. След това, като се фактор на пропорционалност. Качваме се на имота 2 :. която има две идентични редове, и собственост 4 е 0.
6. детерминанта не се променя, ако иска да замени низ колони, както и обратното.
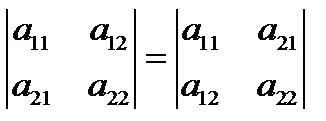
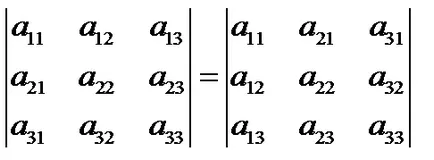
За да се окажат недостатъчни за да се изчисли стойността на детерминантата, стоящи в уравненията в ляво и в дясно.
7. Ако всяка колона елемент (ред) на детерминанта е сумата на две условия, детерминантата може да бъде представена като сума от две фактори, един от които е в колона (ред) е първият от споменатите условия, и от друга - вторият; елементи и на други места, и трите детерминанти на един и същ:
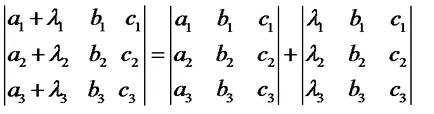
8. детерминанта на матрицата не се променя, ако елементите на ред (колона) матрица за добавяне на елементи от друг ред (колона), предварително умножава по същия номер.
9. детерминанта на продукта от две квадратни матрици е продукт на техните детерминанти :. къде. и - за матрица.