свободно трептене

Математически махало орган, наречен малък размер, суспендиран върху тънък неудължаващ прежда, масата на което е пренебрежимо малък в сравнение с маса тялото. В равновесно положение, когато махалото виси отвес, силата на тежестта базирана на конеца При отклонение на махалото от равновесното положение при φ ъгъл появява тангенциален компонент на силата на тежестта Fτ = -Mg грях φ (Фиг. 2.3.1). "Минус" знак в тази формула означава, че тангенциален компонент насочени в посока, обратна на отклонението на махалото.

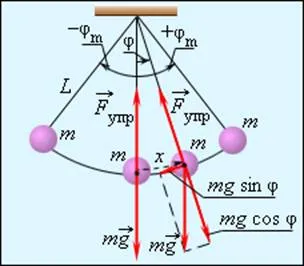
Pendulum. φ - на ъгъл отклонение на махалото от равновесното положение, х = л φ - преместване по дължината на дъгата на махалото

Ако X означава линеен обем на махалото от равновесното положение по протежение на дъга от окръжност с радиус л. неговото ъглово преместване е равна на φ = X / л. вторият закон на Нютон, записани за проекциите на ускорение и сила в посока на допирателната, дава:

Това съотношение показва, че математическото махало е сложна нелинейна система, тъй като силата, има тенденция да се върне махалото към равновесното си положение, е пропорционална не на изместване х. и

Само sluchaemalyh вибрации, когато priblizhennomozhno заменят namatematichesky махало е хармоничен осцилатор. т. е. на система може да изпълнява хармонични трептения. На практика това приближение е валидна за ъгли от порядъка на 15-20 °; когато тази стойност се различава от не повече от 2%. Pendulum с големи амплитуди не е хармоничен.

За малки математически махало трептения втория закон на Нютон може да се запише като

По този начин, тангенциално ускорение aτ махалото е пропорционална на изместване х. взето с обратен знак. Точно това е състояние, при което системата е хармоничен осцилатор. Като общо правило за всички системи, които могат да се възползват безплатно коефициент на пропорционалност хармоничен осцилатор модул между ускорението, а денивелацията от равновесното положение е равен на квадрата на ъгловата честота:

Тази формула изразява естествената честота на малките трептения на математическо махало.

Всеки орган набучени на хоризонтална ос на въртене, може да изпълнява в гравитационно поле свободните трептения и следователно и на махалото. Такава махалото се нарича физическа (Фиг. 2.3.2). Той се различава от математическата само масово разпространение. Позицията на стабилно равновесие маса център С е по-ниска от физически въртене махало ос О на вертикалната линия, минаваща през оста. В случай на φ ъгъл махало настъпва в момента на гравитацията, махалото тенденция да се върне в своето равновесие позиции:

"Минус" знак в тази формула, както обикновено, това означава, че въртящият момент има тенденция да се превърне махалото в обратна посока на отклонение си от неговата равновесна позиция. Както и в случая на един прост махало, който се връща в момента M е пропорционална. Това означава, че само при малки ъгли, когато физическото махало в състояние да извършва безплатни трептения хармоничен. В случай на малки колебания

и втория закон на Нютон за физическо махало е под формата

където ε - ъглово ускорение на махалото, I - инерционен момент на махалото по отношение на оста на въртене О. коефициент модул на пропорционалност между изместване и ускорение равно на квадрата на ъгловата честота:

Тук ω0 - естествена честота на малките трептения на физическо махало.

По-строги извеждане на формули за ω0 и Т може да се направи, ако се вземе предвид връзката между математически ъглово ускорение и ъглово отклонение: ъглово ускорение ε е втората производна на ъглово преместване МФ съществува време:

Поради това уравнение, изразяващо втория закон на Нютон за физическо махало, може да се запише като

Това уравнение е без хармонични трептения.

в това уравнение има смисъла на квадрат коефициент кръгови честоти на хармонични трептения на физическа махало.

Според теоремата на паралелно изместване на оста на въртене (теорема Щайнер) инерционен момент I може да се изрази чрез момента на инерция IC около ос, минаваща през центъра С на масите на махалото и успоредна на оста на въртене:

И накрая, за ъглова честота ω0 на свободни трептения на физическо махало следния израз: