Съотношенията в триъгълник, математика

228. В тази глава, ние основно ще се разбира под наименованието на сегмента AB, AC и така нататък. Г. Изразяване техните номера.

Ние знаем, (стр. 226), че ако се дава геометрично две сегменти А и Б, а след това можем да изградим средна пропорционално между тях. Да предположим сега, че сегментите не са геометрично и номера, т.е.. Е. Съгласно а и б, имаме предвид броя на изразяване 2 сегмент данни. След това намери среден интервал ще бъде намалена пропорционално определяне на съотношението на х а / х = х / б, където А, В и X форми. От тази част, ние имаме:

229. Да предположим, че имаме правоъгълен триъгълник ABC (Юни. 224).

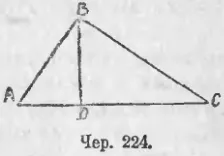
Капка от върха си под прав ъгъл (∠B линия) BD перпендикулярна на хипотенузата АС. . Тогава от 225 знаем:

1) AC / AB = AB / AD 2) AC / BC = BC / DC.

Следователно, ние получаваме:

2 AB = AC · АД и BC 2 = AC · DC.

Сгъваема от двете страни на равенството, получаваме:

AB + BC 2 2 = AC · AD + AC · DC = AC (AD + DC).

т. е. на квадрата на експресиране на хипотенузата е равна на сумата от квадратите на числата експресиращи краката на правоъгълен триъгълник.

За кратко да речем, квадрат на хипотенузата на правоъгълен триъгълник е равен на сбора от квадратите на другите две страни.

Ако се получи в резултат формула, геометричен тълкуването, получаваме запознат теоремата на Питагор (161 п.):

квадратен построен върху хипотенузата на правоъгълен триъгълник, е равна на сумата от квадратите, построени на Catete.

От уравнението AB 2 + BC 2 = AC 2 понякога е необходимо да се намери крака на правоъгълен триъгълник, хипотенузата а от друга крака. Снабдете, напр.:

AB 2 = AC 2 - BC 2 и следи.

230. получава числова съотношението на страните на правоъгълен триъгълник ни позволява да се реши много изчислителни проблеми. Нека да решим някои от тях:

1. Изчислява равностранен триъгълник площ от тази страна от него.

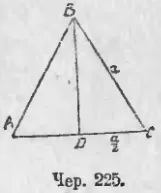
Нека ΔABC (Юни. 225) е равностранен, и всяка страна от него се изразява чрез номера на (AB = BC = AC = а). За да се изчисли площта на този триъгълник трябва да го научат от първа височина BD, което ние наричаме през час. Ние знаем, че в равностранен триъгълник разделя височина BD AC основата на половина, т. Е. AD = DC = а / 2. Ето защо, от правоъгълен триъгълник DBC да има:

2 BD = BC 2 - DC 2

ч 2 = а 2 - на 2/4 = 3а 2/4 (изпълнява изваждане).

(Фактор Transfer под корен).

Следователно, наричайки брой изразим триъгълна зона, чрез Q и знаейки, че районът ΔABC = (AC · BD) / 2, намираме:

Ние можем да погледнем тази формула, като един от начините за измерване на площта на равностранен триъгълник: необходимо е да се измери неговата страна в линейни единици, изграждане номера намерени на площада, умножете това число чрез √3 и се разделя на 4 - получи израз в квадрат площ (съответния) единици.
2. Страните на триъгълника са 10, 17 и 21 линг. е един. Изчислете своята област.

Пропуснете височина ч в нашия триъгълник (Шер 226.) На голяма страна - то със сигурност ще се проведе във вътрешността на триъгълника като триъгълника тъп ъгъл може да се настрои само срещу по-голямата страна. Тогава голяма част = 21, разделен на два сегмента, една от които се обозначават чрез х (виж чертежа.) - тогава другият = 21 - х. Ние получи две правоъгълен триъгълник, от които имаме:

Н2 = 10 2 - х 2 и Н2 = 17 2 - (21 - х) 2

От лява страна на тези уравнения са едни и същи,

10 февруари - 2 х 2 = 17 - (21 - х) 2

Следвайте стъпките, които получаваме:

02 октомври - х 2 = 289-441 + 42x - х 2

Опростяване на това уравнение, ние откриваме:

Тогава от уравнение з 2 = 10 2 - х 2. получаване на:

Н2 = 10 2 - 6 2 = 64

Тогава там е необходимата площ:

Q = (21 · 8) / 2 Quad. е един. = 84 четворни. е един.

3. Възможно е да се реши един често срещан проблем:

как да се изчисли площта на триъгълник на своя страна?

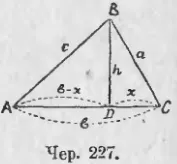
Да предположим триъгълник ABC страна са изразени като брой BC = а, AC = б и АВ = C (Юни. 227). Предполагаме, че АС има голяма страна; След това влезе вътре височината BD ΔABC. Ние казваме: BD = ч, DC = х и след това AD = б - х.

От ΔBDC имаме: з 2 = а 2 - х 2.

От ΔABD са: Н 2 = с 2 - (б - х) 2,

от 2 - х 2 = с 2 - (б - х) 2.

Решаването на това уравнение, получаваме последователно:

2bx = 2 + б 2 - в 2 и X = (2 + б 2 - С2) / 2b.

Освен това, заместване на този израз в уравнение Н = 2 2 - х 2. находка

(Последният е писано въз основа на това 4а числителя 2 б 2 - (2 + б 2 - в 2) 2 може да се разглежда като квадрати равенство, което се разлага от продукта от сумата на разликата).

Тази формула се превръща, чрез въвеждане на периметъра на триъгълник, означен чрез 2p, г. F.

Изваждайки при 2в от двете страни на уравнението, получаваме:

A + B + C - 2в = 2p - 2с или А + В - с = 2 (р - в):

в + а - б = 2 (р - б) и в - A + B = 2 (р - а).

(P изразява semiperimeter триъгълник).
Etoyu формула може да се използва за изчисляване на площта на триъгълник от три страни.

1. Основата на равнобедрен триъгълник е 10 дм. и неговата площ = 60 кв. дм. Намери (изчисляване) периметъра.
2. Паралелни страни на равнобедрен трапец един са равни на 16 и 40 дм. и всеки от неуспоредни страни = 37 дм. Изчислете своята област.
3. Страните на трапеца са равни на паралелен 15 и 36 DM. и nonparallel 13 и 20 дм. Изчислете своя район.
4. Side на ромба и неговия по-малък диагонал същото. Намерете формулата за измерване на площта на модела диамант на едната си страна.
5. Крака на правоъгълен триъгълник са равни съответно на 6 и 8 инча. Намерете дължината на хипотенузата, сключен между ъглополовяща директен ъгъл на триъгълника, а надморската височина, изготвен от върха на правия ъгъл.
6. Ъглополовяща правоъгълен триъгълник хипотенузата на прав ъгъл разделя сегмент в две равни на Lin съответно. е един. Изчислете своята област.
7. Намерете своя страна на площада, е равна на един равнобедрен триъгълник, чиито страни = 12 ½ линг. е един. а височината се отнася до основата, като 2. 3.
8. Страни на успоредник са равни на А и Б и един от неговите ъгли = 45 °. Намерете формула за своята област.
9. ъгъл Паралелограма = 30 °; изрази област чрез своя страна (а и б).

232. Sec. 229 открихме отношенията между двете страни на правоъгълен триъгълник. Можете да намерите подобна връзка на страните (с добавянето на още един сегмент), наклонен правоъгълен триъгълник.

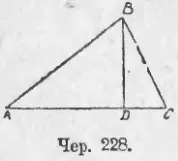
Да предположим, че имаме първи ΔABC (Юни. 228), така че ∠A е остър. Ние ще се опитаме да намерим израз за квадрата на BC, която се намира срещу остър ъгъл (точно както е описано в т. 229 намери израз за квадрата на хипотенузата).

Изграждане на BD ⊥ AC, ние получаваме от правоъгълен триъгълник BDC:

BC 2 = BD 2 + 2 DC

Сменете BD2, определяйки го от ABD, където имаме:

2 BD = AB 2 - АД 2

и да се замени сегмента DC чрез AC - АД (ясно е, че DC = AC - АД). След това ние получаваме:

BC 2 = AB 2 - АД 2 + (AC - АД) = AB 2 2 - АД 2 + AC 2 - 2AC · АД + 2 АД

Следвайте подобни термини, ние откриваме:

BC 2 = AB 2 + AC 2 - 2AC · АД.

Тази формула гласи: квадратен страна на триъгълника, който се намира срещу малък ъгъл, равен на сбора от квадратите на другите си две страни минус удвоеното произведение на някоя от тези страни в горната част на своя сегмент от малък ъгъл на височината.

233. Сега нека ∠A и ΔABC (Юни. 229) тъп. Ние считаме, израз на квадрата на BC, лежащ срещу тъп ъгъл.

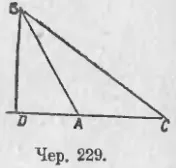
Чрез изграждането на височината BD - сега тя се намира малко по-различно: 228 ∠A където остри точки В и Г са разположени от едната страна на А, както е тук, където ∠A тъпи точки C и D ще бъде разположен от двете страни на правоъгълен А. След това ΔBDC получавате:

BC 2 = BD 2 + 2 DC

Ние може да замени BD2, определяйки го от правоъгълна ΔBDA:

2 BD = AB 2 - АД 2

и сегмент DC = AC + АД, което е очевидно. Заместването, получаваме:

BC 2 = AB 2 - АД 2 + (AC + AD) = AB 2 2 - АД 2 + AC 2 + 2AC · АД + 2 АД

Следвайте подобни термини, ние откриваме:

BC 2 2 = AB + AC 2 + 2AC · АД,

т. е. на квадратен страна на триъгълника, който се намира срещу тъпият ъгъл, равен на сбора от квадратите на другите си две страни, както и два пъти на продукта на един от тях за рязане си от върха на тъпият ъгъл на височината.
Това уравнение, както и формула и стр. 232, позволи геометрична интерпретация, която е лесно да се намери.

234. Използване претенции свойства. 229, 232, 233, ние можем, ако са дадени страна на триъгълника в цифрите, дали предлага триъгълник прав или тъп ъгъл.

Прав или тъп ъгъл в триъгълник може да се постави само срещу по-голямата част, това, което е на ъгъла срещу него, че е лесно да се научат: ъгълът е остър, директно, или ням, според това дали по-голямата част на площада-малко, равно или по-голямо от сбора от квадратите на другите две страни ,

Разберете дали има пряка или тъп ъгъл в следните триъгълници, определени от техните партии:

1) 15 дм. 13 дм. и 14 дм. 2) 20, 29 и 21; 3) 11, 8 и 13; 4) 7, 11 и 15.

235. Нека да успоредник ABCD (Шер 230.); изграждане на диагоналите AC и BD, а височината BK ⊥ АД и CL ⊥ АД.

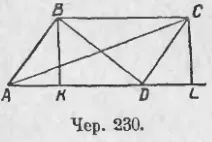
След това, ако ∠A (∠BAD) остър, на ∠D (∠ADC) непременно тъп (поради тяхната сума = 2d). От ΔABD, където ∠A чувстват остър, имаме:

2 BD = AB 2 + AD 2 - 2Ad · AK,

и от ΔACD, където ∠D тъп, ние имаме:

AC 2 = АД 2 2 + CD + 2Ad · DL.

Замяна на последния сегмент на формула АД, равна на отсечката BC и DL равна на АК (DL = АК, за ΔABK = ΔDCL, тъй като лесно се вижда). След това ние получаваме:

AC2 = BC2 + CD2 + 2Ad · AK.

Добавянето на израза за BD2 с последния израз за AC 2. находка:

2 BD + AC = AB 2 2 2 + AD + BC 2 + CD 2

като членовете на -2AD · AK и + 2Ad · AK се изключват взаимно. Ние може да чете полученото уравнение:

Сумата от квадратите на диагоналите на успоредник е равна на сумата от квадратите на страните му.

236. Изчисляването на медианата и ъглополовящата на триъгълника на своите страни. Да предположим триъгълник ABC (Юни. 231) построен средната BM (т. Е. AM = МС). Знаейки ΔABC страна: BC = а, AC = В и АВ = с, за да се изчисли средната BM.

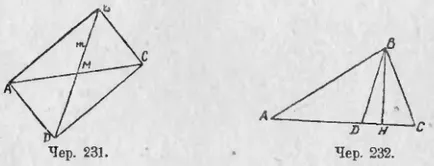
BM ще продължи да се съкращават и нарязани MD = BM. Комбинирането на D с A и D с C, ние получаваме успоредник ABCD (Фигура лесно, тъй като ΔAMD = ΔBMC и ΔAMB = ΔDMC).

Повикване медиана BM през м, ние получаваме BD = 2 m, а след това, с помощта на предходния параграф .:

237. Изчисляване на радиуса на кръга окръжност около триъгълника. Нека около ΔABC (Юни. 233) описва окръжност О. изгради кръг с диаметър BD, BH акорд АД и височина на триъгълник.

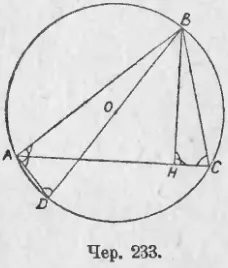
ΔBCH (∠A = ∠H = г - А прав ъгъл, тъй като е вписан, въз основа на диаметъра и BD ∠D = ∠C, като вписан, въз основа на една дъга АВ). Ето защо, ние трябва:

или като се обадите чрез радиус R OB, BH през Височина H и страните AB и BC, както и преди, и С, съответно, чрез:

но областта ΔABC = Q = BH / 2, където Н = 2Q / б.

Следователно, R = (ABC) / (4Q).

Ние можем да (стр. 230 дъно. 3) се изчислява площта на триъгълник Q на своите страни. От това можем да се изчисли R от трите страни на триъгълника.

238. Изчисляване на радиуса на кръга, вписан в триъгълник. Впише в △ ABC, от двете страни на която са (юни 234), обхватът на О. да го свърже с център О на върховете на триъгълник и допирни точки г, Е и F страни на кръга, ние откриваме, че радиусът на OD на кръг, OE и са на височината на триъгълника ВОС, COA и АОВ.

Обаждане през вписан кръг с радиус R, ние имаме: