Съюз на комплекти, теория на множествата, примери за решения

• Асоциация или определя сумата от п A 1. А2. ..., An е на снимачната площадка. състояща се от елементите. включени в поне една от тези п комплекти. А = А1 А2 U U U ... An знак, когато U означава операция съюз на комплекта.

Формално съюз експлоатация на комплекта се определя по следния начин.

където ∨ - логичен знак. обозначаващ съюз или. Прочетете този запис така. Много - всички тези стойности на х. които принадлежат към една и набор А1. или А2 избран. или A3 настроен и така нататък, докато множеството Ап.

За да се изпълни обединението на наборите има калкулатор операции на комплекти.

Например. Нека набор. А1 =; А2 =; A3 =. Прилагането им на Операцията за присъединяване. получаваме нов набор от A = A1 A2 U U = A3. Забележка. че б ∈ A1 и б ∈ A3. обаче множество елемент б включва само веднъж (изземване. всички елементи трябва да са различни).

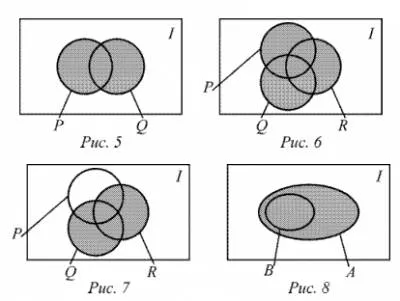
На Вен диаграми (калкулатор) комбиниране на комплектите представляват непрекъснати засенчване области, съответстващи на тези комплекти:

• Фиг. 5 защрихованата зона, определена Q U Р,
• Фиг. 6 показва оцветяване площ множество (Р U Q) U R.
• Фиг. 7 показва три набора от Р, Q и R. защрихованата отбележи множество Q U R.

операция на масивите съюз има следните свойства:

а) съюза е комутативен:

A U B U C = A U C U B = B U A U С, и т.н .;

б) съюза е асоциативен:

(A U В) U C = A U (B U C) = A U B U В.

(.. не могат да бъдат използвани Благодарение на асоциативност при запис на няколко набора от свързани помежду си знак скоби сдружение);

в) ако B ⊆ А или В ⊂ А, тогава U В = А.

Фиг. 8 показва диаграма на Вен на събитието. където В ⊂ A.

Областите в сянка маркирани настроен А, който е

едновременно се прилага към множеството A U Б.

• От собственост "в" трябва да бъде. че:

1. A U А = А;
2. A U А = ∅;
3. A U I = I.

1. Откриване на елементите на комплекта A U Б. Ако

2. Намерете броя на елементите. първо, а след това - А1. след това - А2 (възходящ ред от номер), ако А = 1 ∨ х ∈ А2); A1 ⊂ I - набор от числа. кратни на три; A2 ⊂ I - набор от числа. кратни на четири>; I =.

3. Предвид три групи А, В, С, известни. че ∈ A. Списък на всички верни твърдения.

а) ⊂ В; д) ∈ В;

б) ∈ A U В; х) ⊆ A U В;

а) ⊂ B U С; з) ∈ B U С;

ж) ∈ A U B U С; и) ⊆ A U B U C

Отговори: б), г), д), д), I) - е вярно.

4. На фиг. 9 показва диаграма на Вен трите комплекта. Вземете елементи на определя U Б. а след това - A U В.

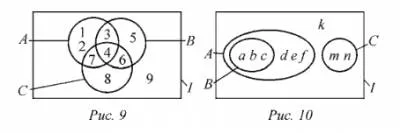
5. Списък елементи на набор М (Фигура 9) .:

6. Списък елементи на N (Фигура 9) .:

7. Списък елементи на K, ако е

8. Списък елементи на набор T (Фигура 9) .:

9. Намерете кардиналността на комплекта A U Б.

Отговор: | А U B | 7 =

10. Намерете броя на кардинал на масивите

A U В, А U C, B U С за диаграма на Вен (фиг. 10).

11. Намерете кардиналността на комплекта A U Б. Ако

Отговор: | А U B | = 5

12. Намери кардиналността на множеството A U Б. Ако А =; B =.

Отговор: | А U B | = 4

13. Виж номер кардинална на серия В (P) U В (Q), където

Отговорът е: | Б (P) U B (Q) | = | B (Р U Q) | = | B| = 04 Февруари = 16

14. Откриване номер кардинална на серия В (К) U В (М), където

15. Колко подходящи подгрупи е настроен. А = А1 U U А2 ... U Ан.

ако А1. A2, ..., An - singletons. по двойки, равна на една от друга.