Силови функции, куб корен, урок по алгебра в 9-ти клас, представяне
Урок и презентация на тема: "Силови функции корен куб корен кубически имоти .."
Определяне на функцията на власт - куб корен
Момчета, ние продължаваме да изучаваме функциите на мощността. Днес ние говорим за функцията на "куб корен на х."
И това, което е коренът на куб?
У брой се нарича куб корен на х (коренът на трета степен), ако $ равенство у ^ 3 = х $.
Означени като $ \ SQRT [3] $, където х - на radicand, 3 - експонента.
$ \ Sqrt [3] = $ 3; $ 3 ^ 3 = $ 27.
$ \ Sqrt [3] = - $ 2; $ (- 2) ^ 3 = -8 $.
Както можем да видим, коренът на куб може да бъде възстановена от отрицателните числа. Оказва се, че нашият корен има за всички номера.
Cube корен от отрицателно число е отрицателно число. Когато издигането знак запазва странно степен, трета степен е странно.
Ние се провери, че: $ \ SQRT [3] $ = - $ \ SQRT [3] $.
Нека $ \ SQRT [3] = A $ и $ \ SQRT [3] = $ б. Ние повишаване на двете изрази в трета степен. $ Х = A ^ 3 $ и $ х = В ^ 3 $. Тогава долара ^ 3 = -b ^ 3 $ или $ а = -b $. Корените на означението се получи желаната идентичност.
Имоти кубични корени
Нека докажем второто имота. $ (\ Sqrt [3]>) ^ 3 = \ Frac ^ 3> = \ Frac $.
Получени, броят на $ \ SQRT [3]> $ куб е равно на $ \ Фрак $ и след това, равен на $ \ SQRT [3]> $, както се изисква.
Момчета, нека да се построи графика на нашата функция.
1) Област на определяне на набор от реални числа.
2) Функцията е странно, тъй като $ \ SQRT [3] = $ - $ \ SQRT [3] $. На следващо място, ние считаме нашата функция като $ h≥0 $, след като графикът ще се отрази за произхода.
3) Функцията увеличава на $ h≥0 $. За нашия функция, по-голямата стойност на аргумента, съответства на по-голяма стойност на функцията, което означава увеличение.
4) функция не е ограничена от горе. В действителност, от произволно голям брой, можете да изчислите корен куб, и ние може да се движи нагоре до безкрайност, се намери повече аргумент стойност.
5) Най-малко $ h≥0 $ стойност е 0. Този имот е очевидна.
Ние изграждане на графиката на функцията в точките на h≥0.
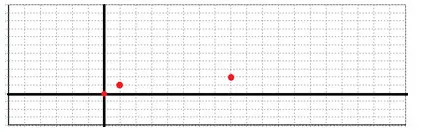
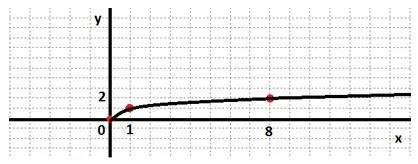
Ние се изгради нашата графика на функцията на своя домейн. Ние помним, че нашата функция е странно.
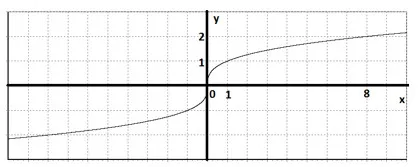
функционални свойства:
1) D (у) = (- ∞ + ∞).
2) нечетен функция.
3) отглеждане на (-∞ + ∞).
4) затваряне.
5) максимални и минимални стойности не са налице.
6) Функцията е непрекъсната по цялата реална линия.
7) E (у) = (-∞ + ∞).
8) изпъкнала надолу (-∞ 0) е изпъкнала нагоре (0 + ∞).
Примери за разтвори мощност функции
примери
1. решаване на уравнение $ \ SQRT [3] = х $.
Решение. Ние изгради две графики на една координатна равнина $ у = \ SQRT [3] $ и $ у = х $.
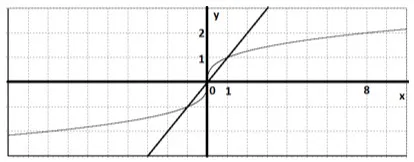
A: (-1, -1), (0, 0), (1, 1).
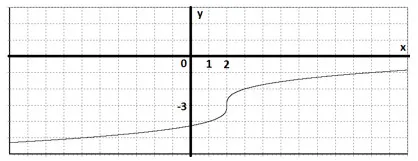
2. Изграждане графика на функцията. $ Y = \ SQRT [3] -3 $.
Решение. Нашата график се получава от графиката на $ у = \ SQRT [3] $ паралелно превод на две единици надясно и три единици надолу.
3. Нанесете функцията и го прочетете. $ \ Beginy = \ SQRT [3], x≥-1 \\ у = -x-2, x≤-1 \ край $.
Решение. Ние се изгради две графики на функции на координатната равнина в съответствие с нашите условия. Когато h≥ $ 1 $ ние парцел корена куб при $ 1 $ h≤ графика на функция линейна.
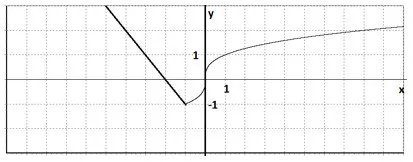
2) Функцията не е нито дори нито странно.
3) намалява в (-∞; 1), се увеличава от (-1 + ∞).
4) затваряне отгоре, ограничена по-долу.
5) голямата стойност не е така. Най-ниската стойност е минус един.
6) Функцията е непрекъсната по цялата реална линия.
7) E (у) = (-1 + ∞).
Задачи за независим решение
1. решаване на уравнение $ \ SQRT [3] = 2-х $.
2. Парцел функцията $ у = \ SQRT [3] 1 + $.
3.Postroit графика на функцията и го прочете. $ \ Beginy = \ SQRT [3], x≥1 \\ у = (х-1) ^ 2 + 1, x≤1 \ край $.