Сборът от ъглите на триъгълник
триъгълника е равна на сумата от степените.
Лесно е да се докаже. Начертайте триъгълник. Чрез един от върховете му се направи линия, успоредна на отсрещната страна и да намерят фигурата равни ъгли. Сравнете с решението в края на статията.
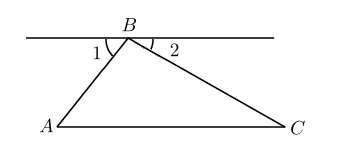
Сборът от ъглите на триъгълник
И ние ще се занимава със задачите на изпита, в който се появява на сумата от ъглите на триъгълник.
- Един от най-външните ъгли на триъгълника е равна градуса. Ъглите не са в съседство с външния ъгъл, се прилага за двете. Намерете най-голямата от тях. Отговор даде градуса.
Външният ъгъл на триъгълника е равна на сумата от двете вътрешни ъгли, които не са в непосредствена близост до него. Следователно, сумата на другите две ъгли на триъгълник е равен градуса, а тяхното съотношение е. Нека тези ъгли са равни, и. получаваме уравнението
Един от ъглите на равнобедрен триъгълник е равен градуса. Намерете някой от другите му ъгли. Отговор даде градуса.
Какво мислите, може ли равнобедрен триъгълник, за да има две степени на ъгъл?
Не, разбира се! В крайна сметка, сумата от ъглите на триъгълник е равен градуса. Следователно, един от ъглите на триъгълник е равен. а другите две са
Фигура ъгъл е. ъгъл е. ъгъл е. Намерете ъгъл. Отговор даде градуса.
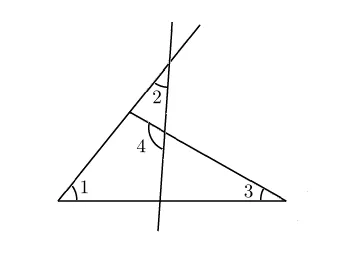
Нека отбележим в чертежа още няколко ъгли. Имаме нужда от тях.
На първо място, ние откриваме, ъгълът 5.
Ъгълът 4, свързан с ъгъл, равен на 7.
Имайте предвид, че този метод на решение - не само един. Просто намери и отбелязване на фигурата всички ъгли, които могат да бъдат намерени.
- ъглите са и двете. Намерете най-малките. Отговор даде градуса.
Нека ъглите на триъгълник са равни. , и. Пишем, каква е сумата на ъглите на този триъгълник.
Как все още може да се докаже, че ъглите на триъгълник е равен на сбора от градуса? Много просто. На тази фигура ъгълът 1 равен на ъгъл (лежат напречно). 2 ъгъл равен на ъгъл C (също лежи напречно). Разширен ъгъл е. Следователно, сумата от ъглите на триъгълник е равен на една и съща степен.