Проверка на разпределението на хипотеза
разпределение изпълнение център.
среднопретеглената
вариации в представянето си.
Абсолютни варианти за изпълнение.
Неточен удар вариант - разликата между максималните и минималните стойности на характеристиката на първичната имунизация.
R = Xmax - Xmin
R = 11 - (-5) = 16
Дисперсия - описва мярка за разпространение за нейната средна стойност (мярка на дисперсия, т.е. отклонението от средната стойност).
Обективна оценка на дисперсията - последователна оценка на дисперсията.
Всяка стойност на серията е различна от средната стойност на 4.82 е не повече от 3,01
Оценка стандартно отклонение.
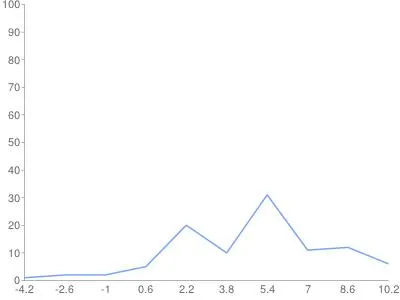
Хистограмата на относителната честота (в%).
Проверка разпределение форма хипотези.
1. За да се тества хипотезата, че X което обикновено се разпространява с помощта на съгласие Пиърсън.
където пи - вероятност за хит в аз-ти интервал на случайна променлива разпределя в зависимост от хипотетично право
За изчисляване на пи вероятности и формула прилага функция таблицата на Лаплас
наблюдавана честота Ni на
пи вероятността да въведете и-ти слот
Очаква честота NPI на
Условията на Pearson статистика Ки
Ние определяме границата на критичната област. От статистиката Pearson измерва разликата между емпиричните и теоретични разпределения, по-голямата му стойност Knabl наблюдава. по-силна е аргумент срещу основния хипотеза.
Следователно, критичната област на тези статистически данни е винаги едностранно: [Kkp + ∞).
Нейните граничните Kkp = # 967; 2 (K-R-1; # 945), ние откриваме, разпределението на таблици "хи-квадрат" и зададени стойности на а, к (брой интервали), R = 2 (XCP параметри S и измерени в пробата).
Kkp = 14.06714; Knabl = 32.73
Наблюдаваното от статистиката Pearson попада в критичната област: Коба> Kkp, така че има основание да се отхвърли нулевата хипотеза. Тези проби не са разпределени нормално.
разпределена плътност График
влизане Правила данни
Задайте своите въпроси или да направите предложения или коментари могат да бъдат долната част на страницата в раздела Disqus.
Можете също така да изпратите заявка за помощ при справянето с изследвания на наши доверени партньори (тук или тук).