Потенциалната енергия във външната напрегнатостта на полето

От израза (4.9) следва, че работата е равна на стъпката на потенциалната функция, и тази работа отива на стъпката на кинетичната енергия на частицата, както е показано (4.5). По този начин,

Ние се придвижат от функция на функция. свързана с отношението

Тогава от (4.11), получаваме :. или.

Този резултат означава, че стойността на частицата в областта на консервативни сили, остава постоянна, т.е. Тя е константа на движение. Функцията се нарича потенциална енергия на една частица в областта на външната сила на полето. По този начин, потенциалната енергия характеризира взаимодействието на частиците с напрегнатост на полето и в зависимост от позицията на частиците в тази област, т.е. координатите.

Стойност. равна на сумата от кинетичната и потенциална енергия, която се нарича общо механичната енергия на частицата.

От израза (4.9) с (4.12), получаваме

-работа на консервативна сфера сили на частиците, равен на намаляването на потенциалната енергия на частицата, т.е. работата се извършва за сметка на потенциалните енергийни резерви. Работата, извършена от консервативните сили в прехода от системата НЯКОИ позиция на нула, се нарича потенциална енергия U на системата в тази позиция.

Експресия (4.7) с (4.12) под формата

силил, в качеството на частицата в стационарна напрегнатостта на полето е равен на градиента на потенциалната енергия на частицата в тази област, се приема с обратен знак.

Нека частица, различна от стационарен потенциал областта на сили, също не-консервативни сили действат. След това, по време на прехода на частицата от точка 1 до точка 2 по-горе, че ще свърши работата, където - работят не-консервативни сили. Работата на консервативните сили е равна на намалението на потенциалната енергия. след това

Общият работата на всички сили, приложени към частицата е за увеличаване на нейната кинетична енергия. или

-работата на не-консервативните сили се изразходват за нарастването на общата механична енергия на частицата.

Потенциална енергия, както и потенциалната функция се определя до произволна константа добавка. Все пак, това не е от значение, тъй като всички функции, включени в потенциален ценности енергия разлика, или техни производни. Във всяка конкретна задача е избран за произхода на потенциалната енергия, която изчисление на енергия са на други позиции. Поради това може да има както положителни, така и отрицателни стойности.

Конкретната форма на функцията зависи от естеството на силовото поле. В областта на гравитацията. която се измерва от произволно ниво.

Разглеждане на система, състояща се от не-взаимодействащи частици в областта на консервативни сили. Всяка частица има кинетична и потенциална енергия на броя на частиците, а след това можем да пишем за всяка частица

Обобщавайки тези изрази за всички частиците се

- общата механична енергия на не-взаимодействащи системи на частиците, които действат само консервативни сили, остава постоянна.

За да се изясни смисъла на геометричната градиент е полезно да се въведе еквипотенциални повърхности. т.е. тези повърхности, на която скаларна функция U остава постоянна: U (X, Y, Z) = CONST.

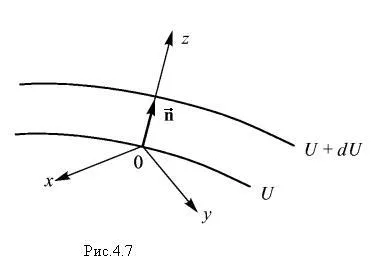
Нека U - един от тези повърхности и да преминава през точка О. пространство, което се определя от наклона (фигура 4.7.). Ние поставяме в този момент на произхода. Z ос е насочена по нормалата към повърхността (- нормално единичен вектор), и X и Y оси лежат в равнина, допирателна към повърхността в точката О. Следователно, в първо приближение, по осите х и у U не променя функцията :. Следователно, тъй като в този случай =. Ако U се увеличава по посока на оста Z. ∂ U / ∂ Z> 0, и следователно, градиента е насочено по нормалата към еквипотенциална повърхност по посока на увеличаване на потенциална енергия. Очевидно е, че в това отношение на потенциалните енергийни промени най-бързо :. По този начин, ние заключаваме, че градиентът на функция скаларна U е вектор насочена перпендикулярно на изравняване на повърхността U (X, Y, Z) = конст в посока на увеличаване на функцията U. дължината му е числено равно на производно на U нормално на еквипотенциални повърхности , Това определение се казва, че инвариант. Това не е структурите зависят от избора на координатна система.

Заедно с изравняване на повърхността през всяка точка в пространството може да се проведе така наречения електропровод. Посоката на допирателната към нея при всяка точка в същата посока като силата, действаща на частиците в тази точка. Очевидно е, че електропроводите и еквипотенциални повърхности са взаимно ортогонални един на друг (фиг. 4.8).

Използването на концепцията за градиент vto.poy закон на Нютон в една точка в областта на сила може да бъде представен като.

Ние сега показват, че от уравнението трябва да е закона за запазване на енергията. тя се размножава за дясната и лявата страна на уравнението в скаларна скоростта на частицата. ,

Изразът в ляво може да бъде пренаписана от време производна на кинетичната енергия на частиците, или чрез прехвърляне на всички от лявата страна, и - получаване на закона за запазване на енергията. Имайте предвид, че получаването тук, това е важно, че потенциалната енергия на частицата не ще зависи изрично по време T (т.е. как). зависимостта от време е бил част от потенциалната енергия е само косвено. през време зависимост от радиус-вектора частици (т.е., как).