Проекцията на вектора на оста

Projection вектор. лежи на оста. по тази ос е броят на абсолютна стойност на дължината на вектор и взема със знак "+", ако посоката на вектора съвпада с посоката на оста, и със знак "-", ако те се противопоставят.

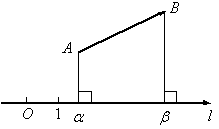
Да предположим, че не се намира по оста, а след това сърчица А и Б са пропуснати вертикалите по оста: получени точки. Векторът се нарича компонент вектор по оста L.

Projection вектор. не лежи на оста. по тази ос се нарича проекцията на неговите компоненти са на тази ос.

др L - проекция на вектор на оста L.

- разширяване на вектора в компоненти по координатните оси.

- Дължина на вектор, изразена по отношение на неговите координати.

Векторът на радиус - вектор, началото на която е в основата. Той има координати.

Ъгъл mezhdui ос L е най-малкия ъгъл между посоката и положителната посока на оста L.

Теорема: проекция вектор върху оста на дължина, равна на вектора на продукт от косинуса на ъгъла между тях.

уюта на посоката - уюта на ъглите, че векторът прави с координатните оси.

Теорема. проекция вектор сума на оста е сумата на проекциите на тези вектори на тази ос.

Теорема: разстоянието между две точки е равен на корен квадратен от сумата от квадратите на разликите на съответните координати.

Теорема: vektorana чрез умножаване на броя на проекция L и умножено по L.

Теорема два вектори са равни, е необходимо и достатъчно, че техните проекции на всяка ос са равни.

Линейна зависимост и независимост на вектори. На базата на

Нека да има п-вектор и п-константа C1, C2 ... .sn.

Вектори се наричат ​​lineynozavisimymi:

1) Ако има C1, C2 ... .sn. от които поне един ненулев, че линейна комбинация е равна на нула.

2) Ако най-малко един вектор на тази система може да се изрази като линейна комбинация от останалите.

Вектори се наричат ​​lineynonezavisimymi:

1) ако комбинацията линеен равно на нула, ако и само ако c1 = с2 = ... = CN = 0.

2) Ако нито един от тези вектори могат да бъдат представени като линейни комбинации от останалите.

Три ненулев вектор, наречен в една равнина. ако те са в една и съща или паралелни равнини.

Основа на самолета и в пространството

Събирането на всеки две lineynonezavisimyh вектори, принадлежащи към тази равнина се нарича основа на тази равнина.

NB! Всеки вектор лежи в тази равнина може да бъде изразена по отношение на тези два вектора.

Събирането на всички три lineynonezavisimyh вектори се нарича основа на пространството.

Основан на пространството чиито вектори взаимно перпендикулярни, и чиято дължина е равна на една, наречена ортонормирана.

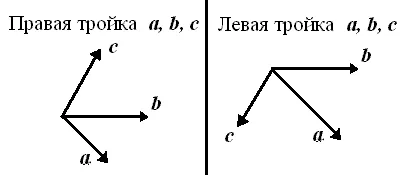
Тройна на вектори се нарича право. ако се гледа от края на най-късата вектор от въртенето е обратна на часовниковата стрелка.

Тройка нарича вектори останали. Ако когато се гледа от края на най-краткия вектор от въртенето се случва в посока на часовниковата стрелка.

Декартово основа. Дължината на основа декартовата вектор

Правоъгълна координатна система в пространството, образуван от три взаимно перпендикулярни координатни оси ОХ, OY и Оз. Осите се пресичат в точка О, който се нарича произход, всяка ос е положителна посока, показана със стрелки, и единични интервали на осите. Единици обикновено са едни и същи за всички оси (което е по избор). ОХ - х-ос. OY - оста у. OZ - на Z-оста.

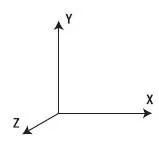
- дължина на вектора изразена по отношение на нейните координати

Скаларни продукт. Изразяване на скаларен продукт на координатите. Физическият смисъл на скаларна продукта

Скаларно произведение и е число, равно на произведението от дължината на тези вектори от косинуса на ъгъла между тях.

Свойствата на скаларен продукт:

·

·

·

·

·

Теорема две ненулеви вектори са ортогонални (перпендикулярно), ако и само ако тяхната скаларен продукт е нула.

Изразяване на скаларен продукт на координатите