Пример за изчисляване на детерминанта

Пример за изчисляване на фактор (фактор) на матрица

В детерминанта на матрицата - полином на елементите на квадратна матрица (матрични елементи, ако този номер, тогава детерминантата на матрицата ще бъде твърде брой).

За намирането на детерминантата на матрицата, първоначалната матрица трябва да бъде квадрат.

Dana 2x2 матрица;

За да се изчисли детерминантата на 2x2 от продукта на елементите на главния диагонал, което трябва да събира, изважда на продукта на вторичните диагоналните елементи;

Dana 3x3 матрица;

За да се изчисли детерминанта на 3x3 е необходимо да се използва формулата;

Ние замени нашите ценности във формулата;

Като се има предвид размера на матрица 4x4;

Има два начина за изчисляване на детерминантата на матрицата:

По дефиниция - чрез разширяване в ред или колона;

По метода на Гаус - привеждане на матрицата да триъгълна форма (този метод е най-добре се използва за решаване на матрицата, размерът на 4х4 и повече).

Нека да решим например първия метод за (по дефиниция - чрез експанзия в ред или колона)

За да се изчисли детерминанта на матрицата, трябва да се използва следната формула, се счита, пример за разширяване на първия ред на матрицата;

Изберете реда или колоната (има такива), най-добре е да изберете ред или колона, където повече нули за изчисляване удобство; В този случай, ние избираме на третия ред, тъй като тя има нула;

Вземете първия елемент на този ред (2); Сега са заличени трета поредна и първата колона;

Ние получи 3x3 матрица;

Съгласно формулата умножим избрания контакт елемент от детерминанта на получената матрица;

Изчисляване на детерминанта на матрица 3x3, ние разгледани в Пример №2

След това, ние правим всички същото като това в етап две, но вземат втория елемент на редицата (0) и заличени третия ред и втората колона;

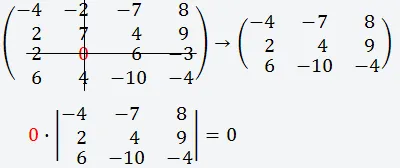
Тъй като този елемент е нула, което не е необходимо да бъдат разгледани, и така всичко е ясно;

Сега да трета линия елемент (6) и заличени третия ред и третата колона;

Ние получи 3x3 матрица;

Изчисли детерминанта на тази матрица и умножено по избрания контакт елемент (6)

Обърнете четвъртата линия елемент (3) и заличени третия ред и четвъртата колона;

Ние получи 3x3 матрица;

Изчисли детерминанта на тази матрица и умножено по избрания контакт елемент (3)

За да се изчисли детерминанта на оригиналната матрица, е необходимо да се определят резултатите;

Ние описваме пример за решение на втория метод (метод на Гаус - привеждане на матрицата да триъгълна форма)

Същността на метода се състои в това, че преди изчисляването на детерминанта причини матрицата на триъгълна форма. Ако в процеса на намаляване на матрица триъгълни ти формира размножават (разделение) линия на броя, след същия брой трябва да бъде умножена (разделена), получен в края на детерминанта;

Пример за намаляване на матрица за триъгълна форма, ние вече обсъдени тук

Така че ние засадени матрица с триъгълна форма;

Сега, за да се изчисли определящ фактор за намаляването на матрицата, е необходимо да се размножават всички елементи по главния диагонал;