Превод на номера от десетична бройна система в друга - системата за брой - общо

При прехвърляне на номера от десетичната система на всяка друга, винаги отделно (по различни правила), преведена цялата и дробната част.

Превод на цялото

За да се превърне номер от десетични числа система на всяка друга, е необходимо да се извърши число разделение въз основа на първоначалния брой на системата брой, в който трябва да бъде преведен на номера. Така важен остатък от деленето и частното. Лично за споделяне на базата толкова дълго, колкото ще има 0. След това всички останки трябва да се напише в обратен ред - това ще бъде броят на новата система за номериране.

Например, превод - 25 номера от десетичното число в двоична система ще бъде, както следва:

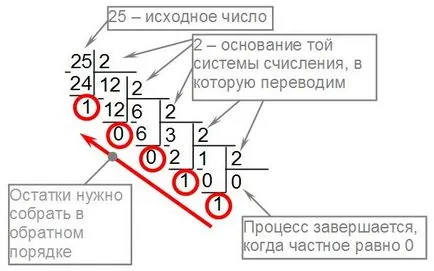
Писане на останките в обратен ред, получаваме 2510 = 110012.

Ако мислите, че за това, лесно можете да забележите, че преводът е абсолютно произволен брой в двоичен бройна система е последният остатък (т.е. първата цифра на резултата) винаги ще бъде равна на най-новите специфични, които се оказаха по-малко от основата на системата на брой, в които превежда номер. Следователно, разделянето често спря пред частния става нула - в момент, когато в частния, така става по-малка база. Например:

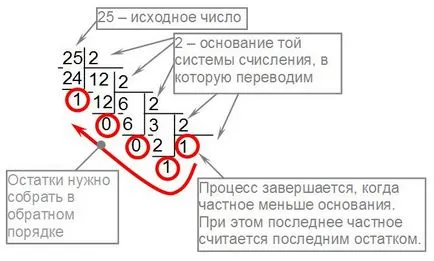
Превод на десетичната система в друга бройна система, направени от едни и същи правила. Ето един пример за превод 39,310 като шестнадесетично число:

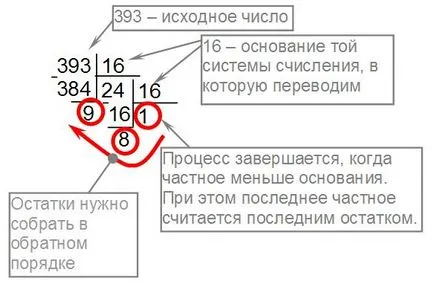
Писане на останките в обратен ред, получаваме 39 310 = 18 916.

Трябва да се разбере, че остатъците, получени в десетичната система. Когато разделен от 16 остатъци могат да възникнат не само 0-9, но и остатъците от 10 до 15. Всяка баланс - е винаги точно една цифра на системата номер, в която прехвърлянето.

Например, ако превода на шестнадесетично число система сте получили такива остатъци (писано в реда, в който те трябва да бъдат записани в броя): 10, 3, 15, 7, в шестнадесетична нотация на тази последователност остатъци ще съответства на броя на A3F716 (Някои грешка рекорден брой като 10315716 - разбира като това е друг номер, и ако е така ще получите, че във всеки брой на шестнадесетични цифри се извежда от а до F).

Превод фракционна част

При прехвърляне на дробна част, за разлика от прехвърлянето на цялата страна - няма нужда да се делят и размножават в основата на системата брой, в който се превежда. В този случай, всеки път, когато отхвърли цялата страна и дробна част - отново умножава. Събиране на цели части в реда на получаването им - вземете дробна част от желаната бройна система.

Една операция умножение дава точно един допълнителен символ в корен, в която се извършва прехвърлянето.

В този случай, има две условия за завършване на процеса:

1) като резултат от умножението на следващия получите нула в дробна част. Ясно е, че по този нула без значение колко много се размножават - той все още ще бъде нула. Това означава, че броят превод от десетичната бройна система до желаната точна.

2) Не всички възможни числа да преведат точно. В този случай обикновено се прехвърля с определена точност. В този случай, първо определя колко знака след десетичната запетая, ще трябва да - това е колко пъти и ще трябва да изпълните операция умножение.

Ето един пример на превода на 0.3910 в двоична система. Точност - 8 бита (в този случай точността на превода е произволно):

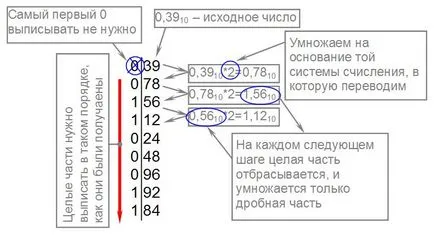
Ако напишете цялата страна в предварителна заявка, ние получаваме 0,3910 = 0.011000112.

Първият нула (показано в синьо удари прозрачни) не е нужно да пиша - защото това не се отнася за дробна част, както и за цялото. Някои погрешно записва нула след десетичната точка, когато се изпуска резултат.

Ето как ще изглежда превод на 0.3910 в шестнадесетичен бройна система. Точност - 8 бита, в този случай точността отново избрани произволно:

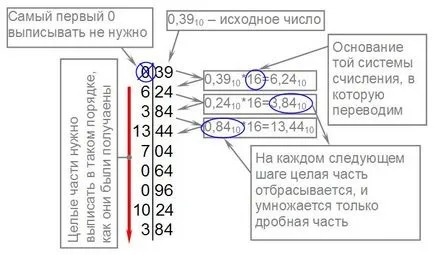
Ако напишете цялата страна в предварителна заявка, ние получаваме 0,3910 = 0.63D700A316.

В този случай, вие вероятно сте забелязали, че цялата страна в размножаването получена в десетичната система. Цялата тази част от получените при превод дробна част от броя трябва да се тълкува по същия начин, като остатъците от превода на цялата част от номера. Това е, ако преведени на шестнадесетично число система на цялото оказа в следния ред: (както някои погрешно понякога записва вместо 0.31371016.) 3, 13, 7, 10, съответния брой ще бъде равна на 0.3D7A16.

Превод на цяло и фракционна част

За да завършите прехвърлянето на цяло и дробна част, трябва да се превежда отделно цялата част и отделно - дробен, и така тези две рекорд заедно.

Например 25.3910 = 11001.011000112 (преводи на цяло число и фракционни части - виж по-горе).

Превод на малки цели числа от десетична в двоична в ума

Защото, когато се работи с различни бройни системи, особено в разработването на програми, това е много често е необходимо да се прехвърлят малки числа, а след това, най-общо казано, че има смисъл да се помни таблицата на съответствие в продължение на първите 16 числа (0 до 15).

Но ако се вгледате, че е лесно да се превежда психически малки числа 0-15 от десетична в двоична, че значителна част от таблицата, която може просто да се изчисли в ума си всеки път, когато това е необходимо. Ние извършваме тази операция много пъти, и в един момент вие ще бъдете в състояние да се разбере - вече сте го запомнила маса или все още се изчисли.

Така че, за да конвертирате малък положителен число от 0 до 15 от около десетични в двоично, първото нещо, за да се разбере - е, че всяка позиция в двоично число съответства на мощността на две. В този случай, с мощност от две за позицията от 0 до 3 Спомням си много прост - това е номер 1, 2, 4 и 8:

Освен това, след десетичната номера, който искате да прехвърлите в двоична система, трябва да бъде представена като сбор от числата 1, 2, 4 и 8, с всеки номер може да се използва не повече от веднъж. Ако си мислиш за него, вие ще разберете, че това може да стане само един-единствен начин.

Когато получите списък с номера, които трябва да влязат в сумата, на позиции, съответстващи на тези числа, трябва да се постави edinichki, останалите - кръстоски. Например, броят 5 - е 4 + 1: