Представяне на графиката на у грях х - синусоида графика на у COS х - косинус
1

2 графика на функция у = грях х - синусоида
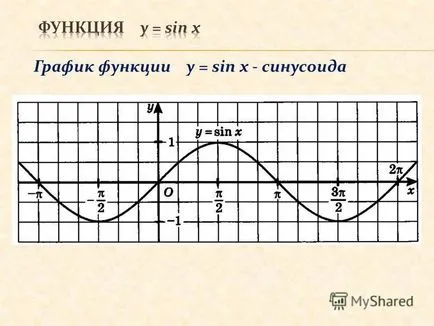
3 Графиката на у = COS х - cosinusoid
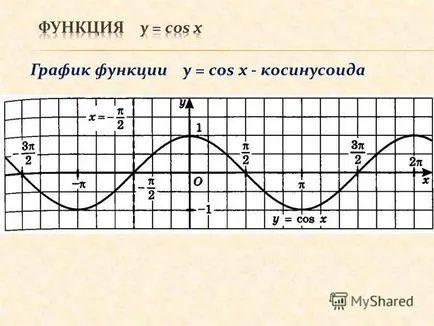
4 графика на у = COS х - Информацията косинус функция: 1.г (у) = (- +) 2.Д. (у) = [- 1; 1] 3. Т = 2π 4. у = COS х - дори функция симетричен по отношение на ординатата на графика 5. защото х = 0 за х = π / 2 + πn, п Z (нули) на интервали от постоянен знак: COS х> 0 в - П / 2 + 2πn при 0 - π / 2 + 2πn
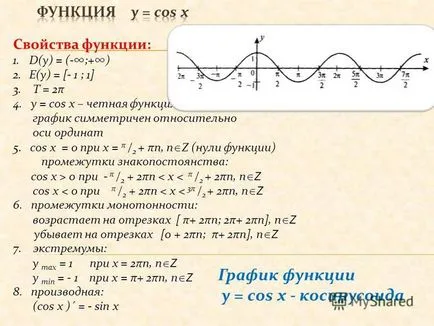
0 + 2πn при 0 0 0 за 5 + 2πn графика на у = грях х - Информацията синусова функция: 1.г (у) = (- +) 2. Е (у) = [- 1; 1] 3. Т = 2π 4. у = грях х - нечетен функция, графиката е симетрична за произход 5. греха х = 0 за х = πn, п Z (нули) грях х> 0 за 0 0 + 2πn при 0 0 + 2πn при 0 + 2πn при 0 0 0 + 2πn при 0 + 2πn
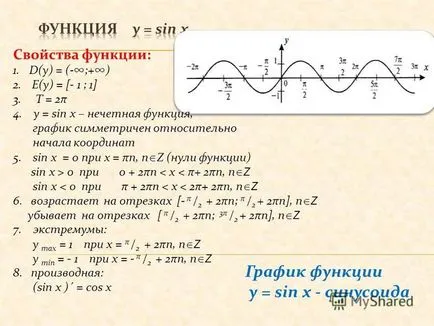
6

7 YX 1 π / 2-π / 2π3π / 22π2π-π-π-3π / 2 -2π 0 у = грях (х + π / 2) Y = грях х строителство функция у = грях (х ± б) Y = грях (х -π / 2)
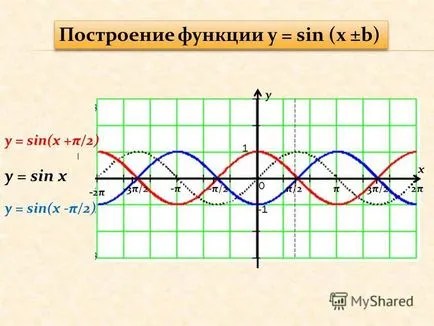
8, у = грях (х + / 4) Графика функция у = грях (х + / 4) Изграждане на функция у = грях (х ± б)
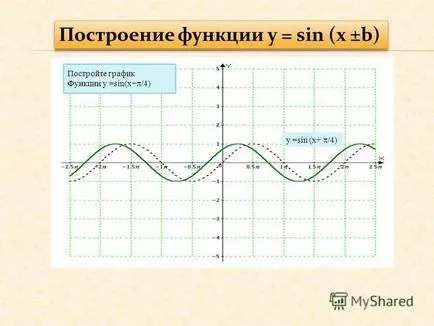
9 Графика функция: у = грях (х - / 6) Y = грях (х - / 6)
10 YX 1 π / 2-π / 2π3π / 22π2π-π-π-3π / 2 -2π 0 у = COS (х -π / 2) Y = COS х строителство функция у = COS (х ± π / 2) Y = COS (х + π / 2)
11 1 у х π / 2-π / 2π3π / 22π2π-π-π-3π / 2 -2π 0 у = грях х 1 у = грях х строителство функция у = грях х ± б у = грях х -1
12 1 у х π / 2-π / 2π3π / 22π2π-π-π-3π / 2 -2π 0 у = защото х 1 у = COS х строителство функция у = COS х ± б у = COS х -1
13 Изграждане на функция у = MSIN х
14 Изграждане на функция у = mcos х
15
16 Изграждане на функция у = грях (к х)
17 Изграждане на функция у = COS (к х)
18 Изграждане на функция у = mcos на (К х)
Определете и 19 б, ако Asos = х + у = б или ASIN х + б. Определете и Ь, ако Asos = х + у = б или ASIN х + б.
Определете и 20 б, ако Asos = х + у = б или ASIN х + б. Определете и Ь, ако Asos = х + у = б или ASIN х + б.
Определете и 21 б, ако Asos = х + у = б или ASIN х + б. Определете и Ь, ако Asos = х + у = б или ASIN х + б.
Определете и 22 б, ако Asos = х + у = б или ASIN х + б. Определете и Ь, ако Asos = х + у = б или ASIN х + б.
Определете и 23 б, ако Asos = (х + б) или у = ASIN (х + Ь). Определете и Ь, ако Asos = (х + б) или у = ASIN (х + Ь).
Определете и 24 б, ако Asos = (х + б) или у = ASIN (х + Ь). Определете и Ь, ако Asos = (х + б) или у = ASIN (х + Ь).
Определете и 25 б, ако Asos = (х + б) или у = ASIN (х + Ь). Определете и Ь, ако Asos = (х + б) или у = ASIN (х + Ь).
Определете и 26 б, ако Asos = (х + б) или у = ASIN (х + Ь). Определете и Ь, ако Asos = (х + б) или у = ASIN (х + Ь).
0 за 0 "заглавие =" Графиката на у = TG х - Информацията tangensoida функции: 1.D (у): 2. Е (у) = 3. Т = π 4. у = TG х - нечетен функция симетричен около графика координира 5. TG х = 0 за х = πn, п Z (нули) на интервали от постоянен знак: TG х> 0 за 0 "клас =" link_thumb "> 27 графиката на у = TG х - свойства tangensoida функции: 1.D ( у): 2. Е (у) = 3. Т = π 4. у = TG х - графика нечетен функция симетричен относно произхода 5. TG х = 0 за х = πn, п Z (нули) на интервали от постоянен знак: TG х> 0 за 0 0 + πn при 0 "> 0 + πn при 0 0 0 за" заглавие = "графиката на у = TG х - свойства tangensoida функции: 1.г (Y): 2. Е (у) = 3. Т = π 4. у = TG х - графика нечетен функция симетричен относно произхода 5. TG х = 0 за х = πn, п Z (нули) на интервали от постоянен знак: TG х> 0 за 0 "> 0 за 0" заглавие = "графиката на у = TG х - свойства tangensoida функции: 1.D (у): 2. Е (у) = 3. Т = π 4. у = TG х - графика нечетен функция симетричен относно произхода 5. TG х = 0 за х = πn, п Z (нули) на интервали от постоянен знак: TG х> 0 за 0 ">
28 графика на у = CTG х - Информацията kotangensoida функции: 1.D (CTG х). 2.E (CTG х) = 3. Т = π 4. у = CTG х - графика нечетен функция симетричен за произход 5. CTG х = 0 за х = пи / 2 + πn, п Z (нули) на интервали от постоянен знак : в TG х> 0 за 0 0 + πn при 0 + πn
При 0 0 0 0 29 като функции Информацията: 1.D (arcsin х) = [1; 1] 2.E (arcsin х) = 3. графика нечетен функция симетричен относно произхода 4. у = 0 за х = 0 (нула) на интервали от постоянен знак: у> 0 в продължение на 0 0 0 0 0 0 0 за за 0 при 0 0 за 0 0 0 за
При 0 -1 0 -1 при 30 Информацията функция: 1.D (ARccOS х) = [1; 1] 2.Д. (ARccOS х) = 3. Не е четен или нечетен 4. у = 0, когато х = 1 (нули) на интервали от постоянен знак: у> 0 в продължение на -1 0 -1 0 -1 при 0 ° С - 1 при 0 -1 0 -1 0, когато най -1
0 за х> 0 у 0 х> 0 у 31 функции Информацията за: 1.D (arctg х) = 2.E (arctg х) = 3. графика нечетен функция симетричен относно произхода 4. у = 0 за х = 1 (нули) на интервали от постоянен знак: г> 0 за х> 0 у 0 за х> 0 у 0 за х> 0 у 0 за х> 0 у 0 за х> 0 у 0 за х> 0 у 0 за х> 0 ш