ponderomotive сили
Кондензатор плочи, противоположно заредени, са привлечени един към друг.
Механични сили, действащи върху заредена макроскопски органи nazyvayutponderomotornymi.
Ние изчисли ponderomotive сили, действащи върху плочите на равнина кондензатор. Има два възможни варианта:
Кондензаторът се зарежда и изключен от заредената батерия (в този случай, броят на такси за плочите остава постоянна р = конст).
Когато премахнете кондензатор плоча от другата работа се извършва
поради което потенциалната енергия на системата се увеличава:
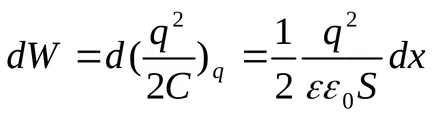
В същото време СР = DW. Приравняването на страните на дясната страна на тези изрази, ние получаваме
В този случай, когато разграничаване между плочите стана ясно разстояние х.
Кондензаторът е заредена, но не е изключено от батерията (в този случай, когато се движат един от кондензатор плоча се поддържа постоянно напрежение (U = конст). В този случай, за отстраняване на единична плочка от други потенциални енергийното поле кондензатор намалява, тъй като има "изтичане" такса с плочи, така че
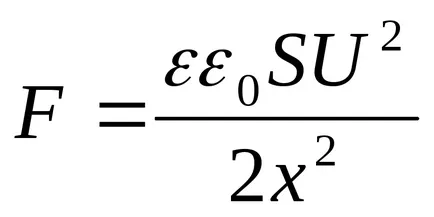
Получената експресията съвпада с формула
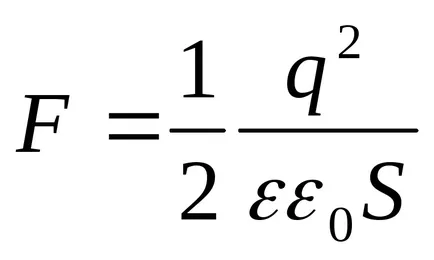
Невярно е еднаква. напрегнатостта на полето на кондензатора е равно на
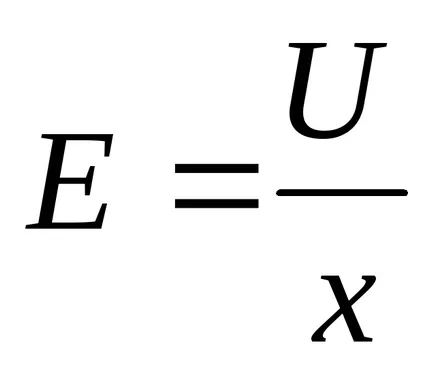
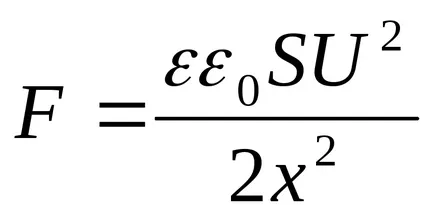
Тези сили не действат само върху плаката. Тъй като плочата, на свой ред натискане на изолатора, поставени между тях и деформира, налягането се произвежда в диелектрика
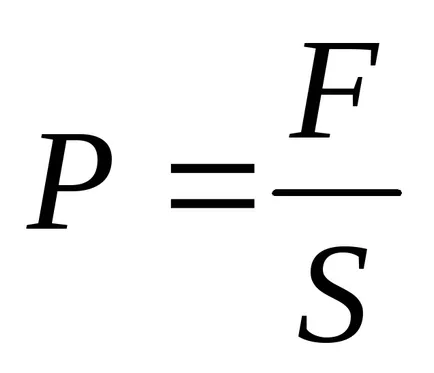
(S - площ на всяка плака).
срещащи налягане в диелектрика и
Примери за решаване на проблеми
Пример 12. 5.K равнина въздушен кондензатор плочи се прилага потенциална разлика от 1.5 кВ. Квадратни плочи 150sm2i разстояние между тях е 5 mm. След изключване на кондензатор от източник на напрежение към пространството между плоските стъкла поставили (ε2 = 7) .Opredelite:
1) потенциалната разлика между плочите след прилагане на диелектрика; 2) капацитет на кондензатор преди и след изолатора; 3) заряд плътността на повърхността на плаките преди и след въвеждането на диелектрика.
Като се има предвид. U1 = 1.5 кВ = 1,5 ∙ 10 3 V; S = 150 см 2 = 1,5 ∙ 10 -2 m 2; ε1 = 1; г = 5mm = 5 ∙ 10 -3 m.
Решение. защото
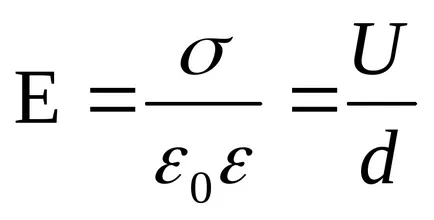
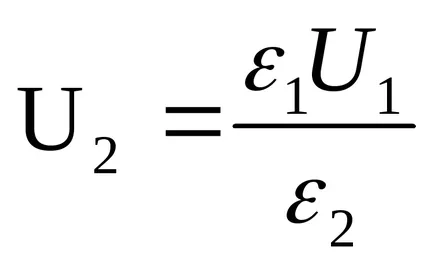
Капацитет на кондензатора преди и след въвеждането на диелектрик
Болт плаки след изключена от източник на напрежение не се променя, т.е. Q = конст. Ето защо, повърхностната плътност такса върху плочите преди и след въвеждането на диелектрик
Пример 12.7. Разликата между плочите на равнина кондензатор е изпълнен с анизотропна диелектрична константа ε на които варира в посока, перпендикулярна на линейно към плаките ε = α + βh от ε1do ε2 освен ε2> ε1. Площта на всеки obkladkiS разстояние между nimid. Намери капацитета на кондензатора.
Решение. Диелектрик pronitsaemostε варира линейно. ε = α + βh където х е измерена от електрода, който постоянно е ε1. Като се има предвид, че ε (0) = ε1. ε (г) = ε2. получаваме зависимостта
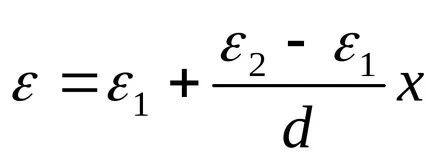
капацитет на кондензатор ще бъде равна
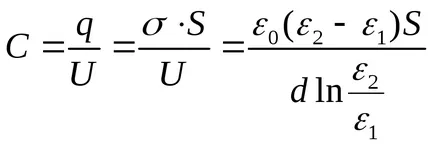
Пример 12.7. Между плочите на равнина, кондензатор, заредена за разлика potentsialovU. успоредна на плочите на двата слоя диелектрик поставени. Дебелината на слоя и диелектрици проницаемост съответно ravnyd1, d2, ε1, ε2. Определяне на интензивността на електростатични полета в диелектричните слоеве.
Решение. Напрежението на кондензатор плочи, тъй като областта в рамките на всяка от диелектрични слоеве е еднакъв,
Електрически изместване в двете диелектрични пласта по същия начин, така че ние може да записва
От изрази (1) и (2) намерите желания
От формула (2) следва, че
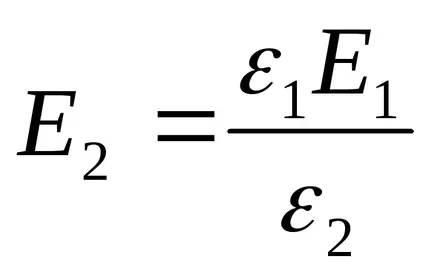
Пример 12.7. Площ plastinSploskogo кондензатор е сто cm2. Пространството между плочите е запълнена с два слоя диелектрик отблизо - на слюда плоча (ε1 = 7) tolschinoyd1 = 3.5 mm и парафин (ε2 = 2) tolschinoyd2 = 5 mm. Определяне на капацитета на кондензатора ..
Решение. капацитет на кондензатор
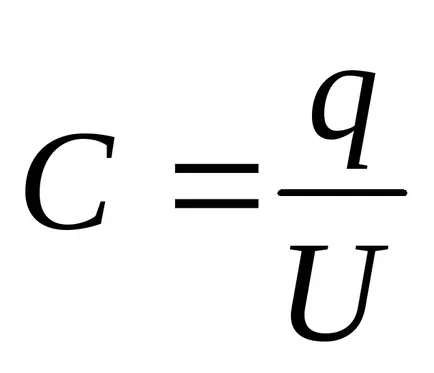
където = - зареждане на плаките кондензатор (- заряд плътност повърхност на плаките); = - потенциални разлики плочи, равен на размера на стрес на диелектричните слоеве: U = U1 + U2. след това
Напрежения U1 и U2 ще намерите формулите
където Е1 и Е2 - интензитет електростатични полета в първия и втория диелектрични слоеве; D - електрическа изместване в диелектрици (същата и в двата случая). Като се има предвид, че
И тъй формула (2), от израза (1) намерите желания капацитет на кондензатор
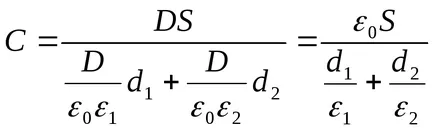
Решение. В поредица свързване на кондензатори такси на всички плочи са равни по сила, така че
Напрежението в кондензатор
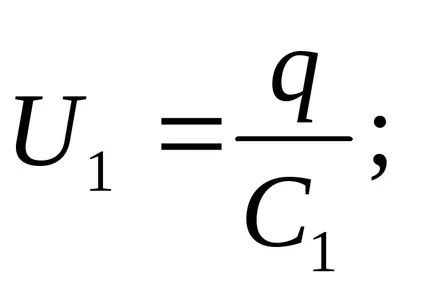
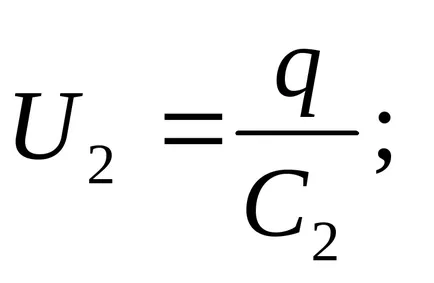
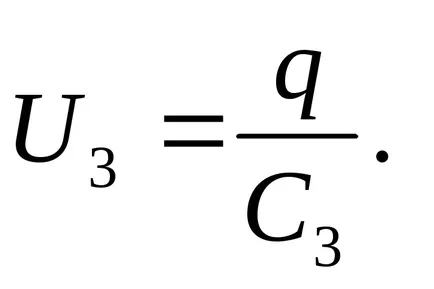
EMF е сумата на изходните напрежения на всяка от серии свързани кондензатори:
При свързване сумират реципрочните капацитет на всяка от кондензатори:
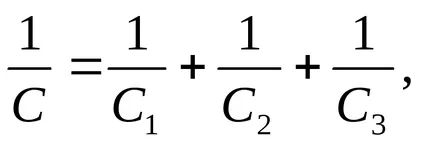
Къде желания капацитет на банката кондензатор
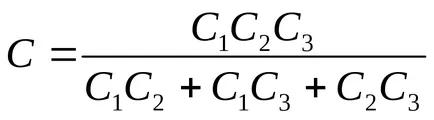
Пример 12.7. Две равнина въздушен кондензатор на същия капацитет са свързани последователно и са свързани към източника на електромагнитни полета. Как и колко пъти да променят заряда на кондензатор, ако един от тях е потопен в масло с диелектрична константа ε = 2,2.
Решение. При свързване такси кондензатор двете кондензатори са равни по сила. Преди потапяне в диелектрика (в масло), таксата за всеки кондензатор
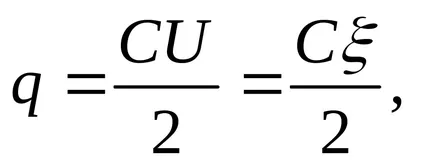
където ξ = U1 + U2 (серия свързване на кондензатори EMF източник на напрежение, равно на сумата от всяка от кондензатори).
След потапяне на една от кондензаторите такси кондензатор диелектрични отново идентични и съответно в първия и втория кондензатори са
(Има предвид, че ε1 = 1), където, ако вземем предвид, че ξ = U1 + U2. намирам
Разделяне (2), като (1), за да намерите желаното съотношение
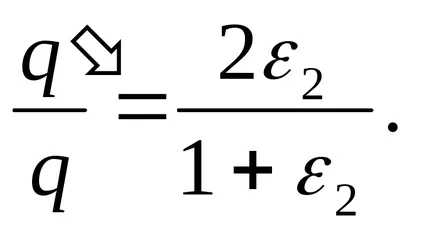
отговори на:
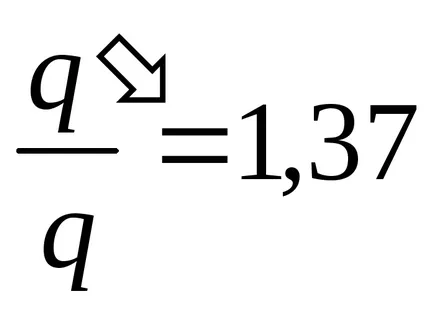
Пример 12.7. капацитети на кондензатори C са свързани помежду си, както е посочено в ris.a. определяне на капацитета Sobschetogo свързване на кондензатори.
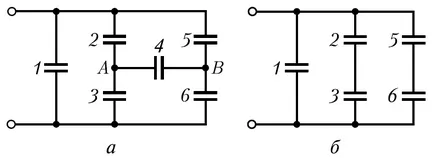
Това схематично три паралелни клона, два от които се състоят от два последователно включени кондензатори
Пример 12.7.Plosky кондензатор въздух капацитет С1 се зарежда 4PF = разлика potentsialovU1 = 100V. След изключване на кондензатор от разстоянието на източник на напрежение между плочите кондензатор увеличени два пъти. Определяне на: 1) разликата potentsialovU2na кондензатор плаки след razdvizheniya; 2) работата на външни сили razdvizheniya плочи.
Решение. Зареждането на кондензатор плочи при изключен от източник на напрежение не се променя, т.е. Q = конст. следователно
където C2 и U2 - и контейнера съответно потенциалната разлика в кондензатор плаки след техните мазане.
Като се има предвид, че капацитетът на плоския кондензатор
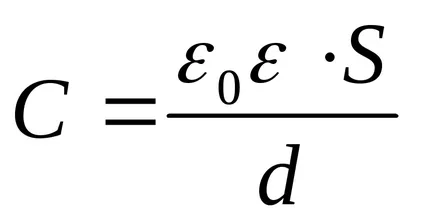
След изключване на кондензатор от системата за източник на напрежение на два заредени плочи може да се разглежда като затворена, за които законът за запазване на енергията: А работата на външните сили е равна на енергията на промяната на системата
където W1 и W2 - съответно кондензатор енергийното поле в началните и крайните страни.
Като се има предвид, че
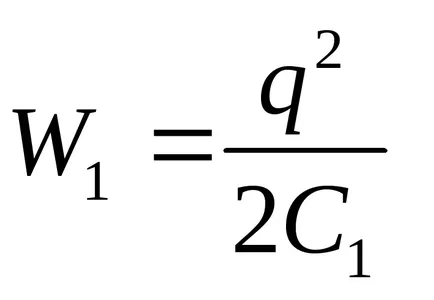
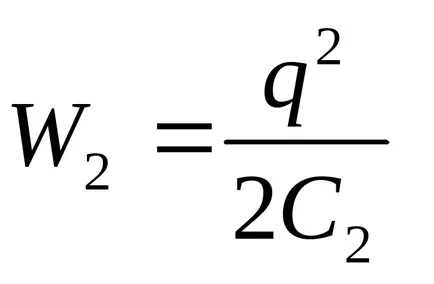
Пример 12.7.Sploshnoy топка диелектрик radiusomR = 5см равномерно зарежда с насипна плътност ρ = 5nKl / m3. Определяне на енергията на електростатично поле, затворено в пространството около топката.
Решение. Невярно е обвинен топка е сферично симетричен, така че плътността на космическата такса е един и същ във всички точки, разположени на равни разстояния от центъра на топката.
E
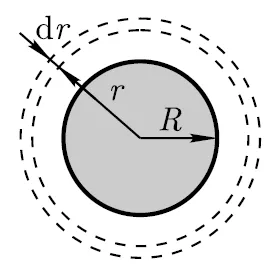
където DV = 4πr 2 р (R - радиусът на сферичната елементарен слой; р - дебелината);
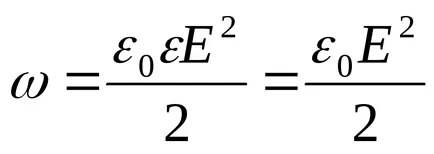
Интензитет E намери от теоремата на Гаус "за областта под вакуум, и в затворена повърхност психически изберете радиус R сфера (вж. Фигура). В този случай, цялата вътрешната повърхност на таксата за топка се присъжда, която генерира съответната област, както и от теоремата на Гаус ",
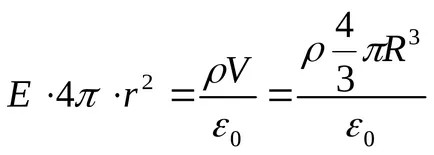
Заместването тези изрази в формула (1), получаваме
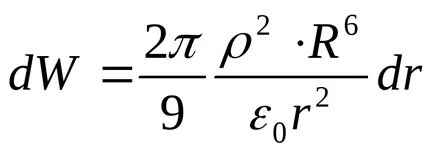
Енергия, съдържащи се в атмосферния пространство топка,
Отговор. W = 6,16 ∙ 10 -13 J.
Пример 12.7.Ploskomu кондензатор с площ obkladokSi разстояние ℓ на съобщена zaryadq. след което кондензатор е изключен от източник на напрежение. Определя кондензатор плочи сила prityazheniyaFmezhdu, ако диелектрична константа на средата между плочите е равна ε.
Решение. Зареждането на кондензатор плочи при изключен от източник на напрежение не се променя, т.е. Q = конст. Да предположим, че по силата на привличане F разстоянието между кондензатор плочи е променен на г ℓ. Тогава сила F върши работа
Според закона за запазване на енергията, тази работа е равна на енергията загубата на кондензатор, т.е.
където, въз основа на изразите (1) и (2), получаваме
Заместването на експресията на енергията на зарежда кондензатор
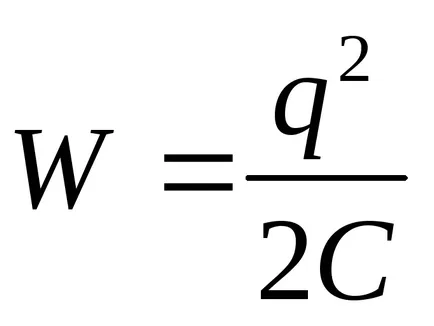
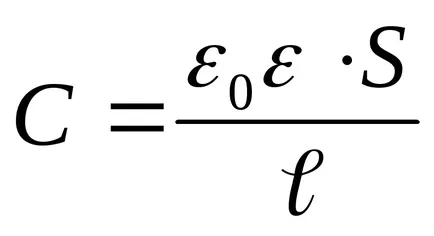
Заместването в (3) на стойността на енергия (4) и извършване на диференциацията, ние откриваме необходимата притегателната сила между кондензатор плочи
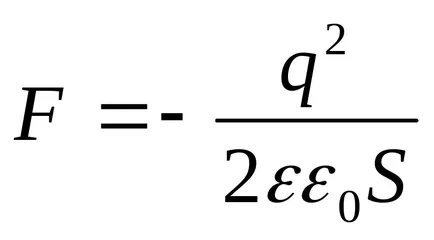
където "-" знак показва, че сила F е силата на привличане.
Пример 12.7.Plosky кондензатор област obkladokSi разстояние ℓ свързан към постоянен napryazheniyaU. Определя кондензатор плочи сила prityazheniyaFmezhdu, ако диелектрична константа на средата между плочите е равна ε.
Решение. Според проблем състояние на плаките кондензатор поддържат в постоянно напрежение, т.е. U = конст. Да предположим, че по силата на привличане F разстоянието между кондензатор плочи променен на dℓ. Тогава сила F върши работа
Според закона за запазване на енергията, работата в този случай продължава да се увеличи мощността кондензатор (за сравнение с предишното упражнение), т.е.
където, въз основа на изразите (1) и (2), получаваме
Заместването на експресията на енергията на кондензатор
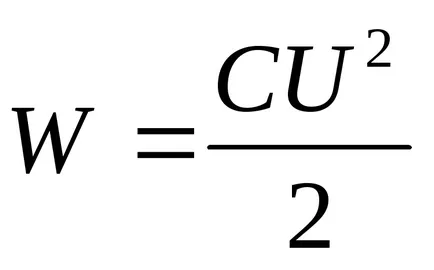
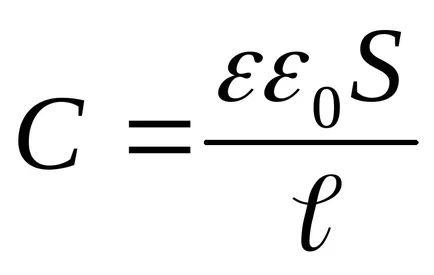
Заместването в (3) на стойността на енергия (4) и извършване на диференциацията, ние откриваме необходимата притегателната сила между кондензатор плочи
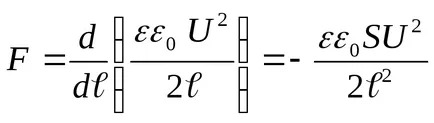
където "-" знак показва, че сила F е силата на привличане.