Polyhedra вписан в една сфера - представяне 152819-1

<<Сфера, описанная около курносого додекэдра

Polyhedra вписан в една сфера >>

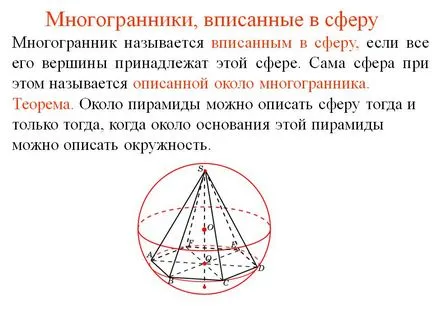
Polyhedra вписан в сфера. А полихедронов се нарича вписан сфера, ако всички негови възли са част от тази област. Самата Sphere е тогава, наречена описан около многостен. Теорема. Около пирамиди могат да опишат обхвата и само тогава, когато в близост до дъното на пирамидата могат да бъдат описани като кръг.

Slide 1 на презентацията "polyhedra вписан в сфера"

Размер: 720 х 540 пиксела формат. JPG. За да изтеглите слайда за използване в класната стая, щракнете с дясното изображение бутон на мишката и натиснете бутона "Съхраняване изображението като. ". Изтеглете цялата презентация "polyhedra вписан в sferu.ppt" може да бъде в цип архив размер на 2246 KB.

Свързано представяне

"Симетрия редовен polyhedra" - Всеки връх на icosahedron е на върха на петте триъгълници. Ледени кристали. Тайната вечеря. Има само пет редовни polyhedra: Микеланджело. се счита Всяка точка на линията и да е симетрична на себе си. Следователно, сумата от равнина ъгли за всеки връх равен на 180 °. Следователно, сумата от плоски ъгли на всеки връх е равен на 324 °.

"Редовно polyhedra" - Голям звездовиден додекаедър. Започвайки лема. Голям icosahedron. Бипирамидални Тороидална Geksadekaedr (BTG) - геометричен модел ATG S. индекс симетрия подгрупа в група automorphism. Стол в триизмерното пространство, със самостоятелно кръстовища. Кеплер-Поансо polyhedra (не от вида на обхвата!). Никой automorphism ATG, с изключение на идентичността не е реализиран геометрично.

"Вписана окръжност" - вписан кръг. На задача номер 1. Доказателство: Номерът на задача 2. Само един кръг може да се впише в триъгълник! Теорема: кръг, може да се впише във всеки триъгълник. Във всеки тангенциален четириъгълник сумата от противоположните страни са равни. Забележки: 2) Не всеки четириъгълник може да се впише окръжност.

"Polyhedron" - октаедър. AB е ръб на куба. А е на върха на куба. Tetrahedron. Polyhedra. Oblique призма. Призми са преки и косвени. AB - височина. Лице на куба е квадрат. Изпъкнал многостен се намира от едната страна на равнината на всеки от неговите страни. Ръчни страни се наричат ​​ръбове. Не-изпъкнал polyhedra разположени на противоположни страни на равнината.

"Вписан ъгъл" - Знаейки как изрази. 2 метод. Следствие 1: Изграждане: __ __ D = А. Цел: Експресна периферен ъгъл стойност, повторение на материала. Доказателство: 3 случай. Големината на периферен ъгъл. Практическа работа. Сравни размера на външния ъгъл и ъгъла в основата. Урок Тема: Погледнато факт: решение. Урок.

"Сграда polyhedra" - Изграждане на редовен тетраедър. Дюрер. Платон. Tetrahedron. Евклид. В додекаедър: 12 лица, 20 върхове и 30 ръбове. От живота на Евклид не знаем почти нищо. Cube. Додекаедър. Изграждане на използване на куба. Плато (Платон). Звездовидни редовен polyhedra. Октаедър. В октаедър: 8 лица, 6 върхове и 12 ръбове.