Подготовка на учениците за изпита и OGE (ДПА) в резолюцията на център за обучение (наръчник по математика -

скорост на тялото. Средната скорост на тялото

Решението за задачи за движение на базата на добре познатата формула на физиката, разбира се

Ви позволява да намерите пътя S. пътува във времето т тяло се движи с постоянна скорост с.

Веднага направи важна

Забележка 1. Единици количества S. тона и обем трябва да бъдат координирани. Например, ако по пътя се измерва в километри. а времето - в часове. след това скоростта трябва да се измерва в км / ч.

В случаите, когато тялото се движи с различна скорост в различните участъци на пътя. въвежда понятието средна скорост. която се изчислява по формулата

Например, ако тялото се движи със скорост v1 време на време Т1. t2 в движещ се със скорост v2 с течение на времето. за време t3 се премести на по-v3 скорост. средната скорост

Задача 1. Планирана треньор на мотора трябва да мине път 100 километра с една и съща скорост и без прекъсване. Въпреки това, ще половината път, автобусът е бил принуден да спре в продължение на 25 минути. С цел да пристигне навреме в местоназначението, водачът на автобус през втората половина на маршрута е увеличил скоростта от 20 км / ч. Каква е скоростта на графика на автобус?

Решение. Ние означаваме с обем на скоростта на графика на автобус, и приемем, че скоростта V, измерено в км / ч. Тя изобразява данните, дадени в проблема 1 на фигура 1.

- по време на графика за автобус (часове);

- времето, през което автобусът преминал през първата половина на пътя (в часове);

V + 20 - автобус скорост през втората половина на пътя (в км / ч);

- времето, през което е управлявал автобуса през втората половина на пътя (в часове).

В изявление проблем даден момент автобусна спирка - 25 минути. Тя трябва да бъде изразено в часове, че всички уреди са били договорени:

Вече можете да създавате уравнение основава на факта, че в автобуса пристигнаха до вашата дестинация на време, а оттам и времето, през което той е бил на пътя, както и времето, за да спре трябва да е равно на времето на графика на автобус:

Ние да решим това уравнение:

По смисъла на първата коренът на проблема трябва да бъде изхвърлена.

Задача 2. (MIOO) Първа час кола, движеща се 120 км / ч, следващите три часа - със скорост от 105 km / h, а след три часа - от скорост 65 km / h. Намерете средната скорост на превозното средство по време на пътуването.

Решение. Използване на формула (2). получавам

Задача 3. През първата половина на пътя на влака е бил със скорост от 40 км / час и половина път - при скорост от 60 km / h. Намерете средната скорост на влака по пътя.

Решение. Ние означаваме с S цялата дължина на пътя, изразено в километри. Тя изобразява данните, дадени в проблема 3, на фигура 2.

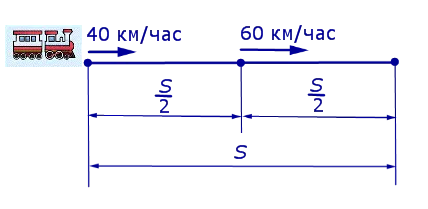
- времето, през което влакът преминал през първата половина на пътя, изразено в часове;

- времето, през което влакът преминава през втората половина на пътя, изразено в часове.

Следователно времето, през което влакът пътува по целия път, както и

В съответствие с формула (1), средната скорост на влака по време на целия път

Забележка 2. Средната скорост на влака в задача 3 е 48 km / h, а не 50 км / час, като понякога се смятат погрешно, се изчислява средноаритметичната стойност на числата (скорост) на 40 km / h и 60 km / h. Средната скорост не е равен на средната аритметична стойност скорости, и е стойност, изчислена по формулата (1).

трафика на реката. скорост на речния отток

За разлика от цели за развитието на страната, в проблемите на движението на реката има нова стойност - скоростта на течението на реката.

Във връзка с банката, която е неподвижна, скоростта на тялото. движещи се по протежение на реката. е сумата от собствената скорост на организма (скорост на тялото в езерото, скоростта на тялото в неподвижна вода, скоростта на тялото в застояла вода) и честота на речния отток. По отношение на брега на скоростта на тялото. движещи се срещу течението на реката. равна на разликата между собствената скорост на тялото и скоростта на течението на реката.

Задача 4: моторна лодка пресече река на 14 км, а след 9 km нагоре по течението, прекарвайки целия път 05:00. моторна лодка в неподвижна вода 5 km / h. Намерете скоростта на течението на реката.

Решение. Ние означаваме с обем на скоростта на течението на реката и да приемем, че скоростта V, измерено в км / данни chas.Izobrazim дадени в проблема 4 на фигура 3.

5 + V - скорост, при която лодката е реката (km / h);

- движението на лодки по реката (в часове);

5 - V - скоростта, с която лодката отиде срещу течението на реката (км / ч);

- движението на лодката срещу течението на реката (в часове);

Сега можете да приравняваме като се вземе предвид факта, че лодката е на път 05:00:

Ние да решим това уравнение:

По смисъла на първата коренът на проблема трябва да бъде изхвърлена.

Задача 5 (Bureau "Quantum") моторна лодка преминава по протежение на река на 34 км и 39 км нагоре по течението, прекарва толкова време, колкото е необходимо да премине 75 км в застояла вода. Намерете отношението на скоростта на лодката в неподвижна вода със скоростта на течението на реката.

Решение. Означаваме Vc (км / ч) на скоростта на лодката в неподвижна вода и оставете Vp (км / ч) скоростта на течението на реката. Ние представляваме данните на задачата 5 на фигури 4 и 5.

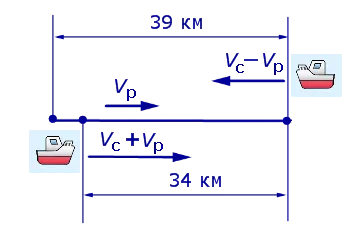
Предвид факта, че и в двете ситуации, лодката се проведе на пътя в същото време, че е възможно да се направи уравнението:

Увеличаването уравнение (4), за да Vp. получаваме

По смисъла на първата коренът на проблема трябва да бъде изхвърлена.

Движение на пръстеновидни писти

Задача 6. (www.reshuege.ru) от точка А кръгова дължина 46 km маршрут пътува колоездач, и след 20 минути от точка А зад колоездача от мотоциклетист. След 5 минути след прилагане на мотоциклетист хванат колоездач за първи път, а след още 46 минути след това, ездач хванат колоездач втори път. Намерете скоростта на велосипедистите и мотоциклетистите.

Решение. По времето, когато за първи път ездач хванат велосипедист, мотоциклетист езда 5 минути и 25 минути колоездач езда, и те пътували по същия път. От това следва, че скоростта на мотоциклетист е 5 пъти по-висока скорост на велосипедиста.

По този начин, сочещ писмо V (км / ч) скоростта на велосипедиста, ние откриваме, че мотоциклетистът е 5 V скорост (км / ч).

Състоянието на дадена задача за времето между две последователни заседания на мотоциклетисти и велосипедисти - 46 минути. Този път трябва да бъде изразено в часове, че всички уреди са били договорени:

Ние представляваме данните на проблема, свързани с движението на водача и на ездача между първия и втория срещи, на фигура 6.

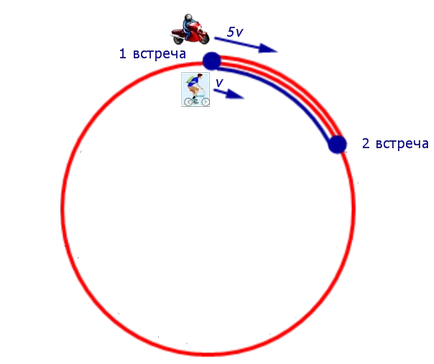
Тъй като по време на часовете, изминали от първата среща, докато на втората среща, мотоциклетист закара на 46 км (цялата кръгов маршрут), плюс пътя, който колоездачът качи за един час, можете да направите следното уравнение:

Решаването на това уравнение, ние откриваме, че скоростта на велосипедиста:

Отговор. Велосипедистът скорост от 15 км / ч, скорост ездач 75 km / ч.

Задача 7. По пътя, който е с дължина на обиколката от 60 km, параграфи А и Б са диаметрално противоположни точки. В колоездач отиде от точка А и направих две обиколки. Първи кръг тя премина с постоянна скорост, а след това намалява скоростта с 5 км / ч. Времето между два пасажа на велосипедиста през точка В е равно на 5 часа. Намерете скоростта, с която водачът премина първия кръг.

Решение. За определеност приемем, че велосипедистът се движи в кръг по посока на часовниковата стрелка и разгледа фигура 7.

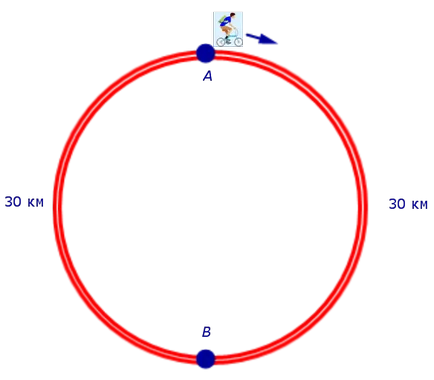
Ако ние означаваме писмо V (км / ч) скорост, при която водачът премина първия кръг, а след това скоростта на велосипедиста на втория тур ще бъде равен на V - 5 (км / ч) и може да се направи на уравнението

Решаването на това уравнение, ние откриваме, че скоростта на велосипедиста в първата обиколка:

Тъй като скоростта на колоездача върху първия диск е по-голяма от 5 км / час, след първата основата трябва да се изхвърли.

Техники, използвани за решаване на проблемите в изпълнението на строителните работи, представени в участъка от нашето ръководство "Предизвикателства за изпълнението на строителните работи."

С примери за решения на проблемите, смеси, сплави и решения могат да бъдат намерени в секцията ни директория "Проблеми на смеси, сплави и решения."

За студенти, които искат да се подготвят добре и да мине изпита или OGE (ДПА) в областта на математиката, физиката или български език за най-висок резултат, на център за обучение "противовъзпалително" притежава