Особености капачка затваря и процесите в тях, страница 2

.

функция Импулс отговор е изчерпателна ОСП динамична характеристика, в смисъл, че той знае, че винаги е възможно да се определи отговора SAR и да е влияние.

Определянето на предавателната функция, следва, че в (2), ще бъде най-, или лапласова снимки:

за (вж. Таблица 2.1).

Замествайки тези изрази в (2), откриваме, че

.

Ако този израз се прилага обратна Трансформация на Лаплас, след това от лявата страна, съгласно (3) имаме функция на импулсната реакция, и от дясната страна - производно на прехода на функция на времето (виж Таблица 2.2.):

ATS уравнение във времевия домейн може да бъде получена чрез прилагане (2) Inverse Трансформация на Лаплас и използва намотка теорема (Таблица 2.2):

.

Спомнете си, че функциите са оригиналите, разполага че с отрицателен аргумент нула.

Качествено времето характеристики на затворен ATS имат формата, показана на фигура 4.6. Когато този трансфер функция H (т) на затворената система има следните характеристики:

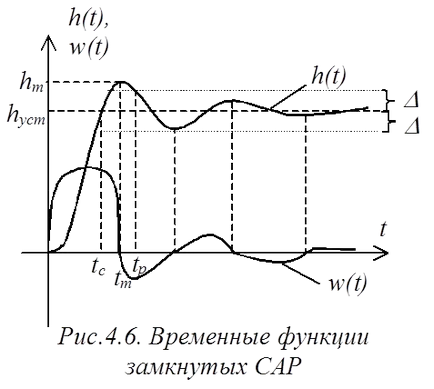
hSet - стационарно състояние стойност на функцията за преход (контролирано координати);

хм - максимална стойност;

D - стойността определяне квартал hSet. в рамките на която може да се разглежда процеса, както е установено (обикновено в технически системи);

TC - първият координацията на функцията за преход, за да настроите стойността;

TM - време за достигане на функцията преход стойности HM;

TP - контрол на времето, след което процесът на преход ще влезе в зона и повече от него ще дойде.

Предварителни данни TC. TM. TP характеризира изпълнението на ДАБ.

трептене CAP характеризира с надвишаването. които обикновено се измерва като процент:

.

Концепцията за свободния и постоянен процес.

ATS реакция (Фигура 4.5) с произволна експозиция може да бъде определена от израза:

където Т - мониторинг време на реакцията на RAA.

Както е известно от SOC на честота, преходно в нормално функционираща система на всички стойности (SAR координати) се състоят от постоянни (вътрешно) и безплатни компоненти.

По този начин за дадената ATS ако оставим на израза (1) ще бъдат принудени да се опише този процес. което се случва, след като всички компоненти на свободните затихване

.

Пример 1. За да се определи принуден ATS процес в Fig.4.5 с спастичен експозиция (фигура 4.7):

.

,

защото. Вторият фактор е нищо друго освен ATS на PD, т.е. ,

От тази формула е ясно, че в процеса на принудително излагане пулсиращ е независима от време и пропорционално на зоната, ограничена от импулсната характеристика на ATS:

.

По този начин, процес, предизвикана от DC (подскача) експозицията е продукт на степента на този ефект на PD при.

Същият резултат може да се получи, ако се вземе предвид, че в този пример (Таблица 2.1), и използване на теоремата крайна стойност (Таблица 2.2), при което

.

Например, Фигура 4.8 за процеса на CAP ще бъдат принудени да:

.

Пример 2. За да се определи кога хармонична действие принуден процес

.

.

.

Вторият фактор е PF ОСП в.

.

Зависимост се нарича честота на предавателната функция на ЗУТ.

По този начин, в процеса на принудително хармонично действие също е хармонична честота и е равна на произведението на функцията за въвеждане на експлоатация.

характеристики честота и физическата им значение

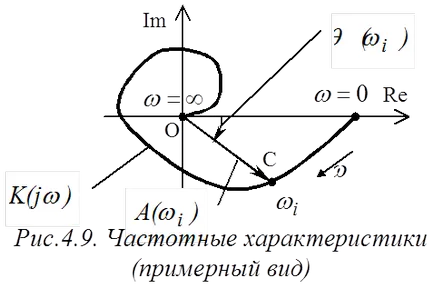
Честота функция SAR е графично изобразени на комплекса равнина при смяна на хармонични честоти на сигнала от нула (или от) преди (фигура 4.9). Подобна схема се промени функцията позиция локус честота, докато промяна на честотата се нарича честотна характеристика.

Честотната могат да бъдат представени, както следва:

,

където - амплитуда честота характеристика (AFC) RAA равно на дължината на честотната характеристика локус (фигура 4.9);

- фаза на отговор (PFC) RAA равно ъглово положение на мястото на честотната (фигура 4.9).

По този начин, реакцията на честота е фактор трансфер между амплитудата на хармонична на входния сигнал и амплитудата на изходния сигнал. С други думи, стойност на честотата отговор на определена честота хармонична на входния сигнал е съотношението на продукцията амплитуда на амплитудата на входния сигнал.

FRF характеризира изместване на фазата на изходния сигнал вълна спрямо входа. Ако изходния сигнал изостава фазата на входния сигнал, в противен случай - напред.

Така, ако ATS се задейства, когато входният действие след преходна изходния сигнал ще има формата:

.

Пример. Построява честота характеристика на капачка с PF

,

където - някои коефициенти.

Решение. Напиши изрази за честотните характеристики:

;

;

.

Въз основа на комплексната равнина при промяна от 0 до (/фиг.4.10/) Keypoint:

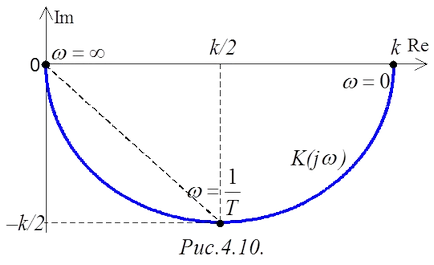
Очевидно е, че честотата намалява с увеличението, но се увеличава. В действителност, честотната ще бъде във формата на полукръг (/фиг.4.10/). Графично и съща честота на изображението и фаза отговор ще бъде много неудобно за възприятието, обаче се използва така наречения логаритмична честотна характеристика.

характеристика на логаритмичната амплитуда честота (LACHH) се нарича връзка

,

който е конструиран в LG W оси. L (фигура 4.11).

Логаритмична фаза отговор (LFCHH) е зависимостта, която е изработена LG w оси. Q (фигура 4.11).

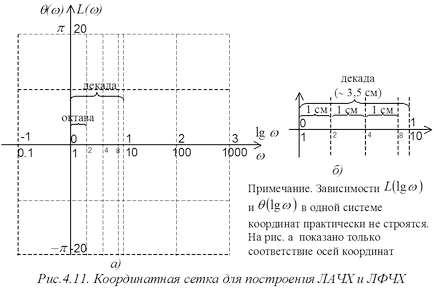
Сегментът на абсцисата, което съответства на увеличение на честотата на 2 пъти, наречена октава; съответно увеличение в честотата 10 пъти - десет години.

При изграждането LACHH и LFCHH ръчно на хартия в клетка, можете да използвате приблизителна октава отношения и десетилетие даден на ris.4.11b.

Например, за горния пример, когато к = 2. Т = 0,1 LACHH LFCHH и имат формата, показана в ris.4.12.

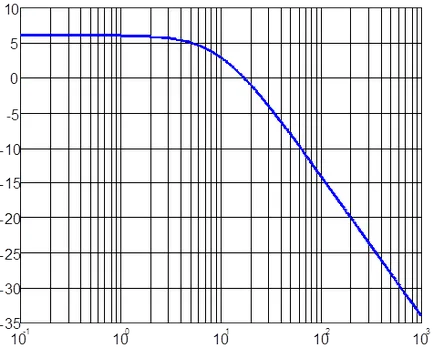
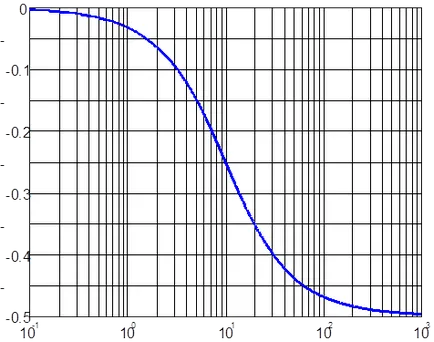
Ris.4.12. LACHH (а) и LFCHH (б) например на ATS.