Определен интеграл и интегрални суми

3. Определянето на интеграла
И неразделна сума

"Само като се приема безкрайно малка единица за наблюдение - диференциал на историята, който е хомогенен и желанието на хората, които достигат за интегриране на изкуството (да вземат сумите на тези безкрайно малки), можем да се надяваме закони postignovenie история."

LN Толстой "Война и мир". Епилог.

Интегрално смятане - клон на математиката, чиято поява е свързана с концепцията за определен интеграл. Имаше интегрално смятане на задачи за определяне на площи и обеми. За да се убедите, помислете за следния проблем.

Да предположим, че трябва да се изчисли обема на лимон. Тя е с неправилна форма и се прилага там всеки известен формула не може обем. Можете да намерите силата на звука чрез претегляне и използването на формули, но лимон плътност в различни части различни. Можете да се процедира както следва. Нарежете лимона на тънки филийки. Всяка парче може да бъде приблизително разглежда като цилиндър с малка височина. Обемът на всяка такава цилиндър лесно изчислява при използване на известни формула. Добавянето на размера на малки цилиндри, ние получаваме приблизителна стойност на целия обем на цилиндъра. Сближаване ще бъде по-точен от по-тънките резени лимон ние отрязани. Този метод на изчисляване на обемите, предлагани в по-III. пр.н.е. Архимед. Гениалният съзнанието на древните гърци очаква много открития XVII-XVIII век.

Между другото, идеята за неопределен интеграл се появява много по-късно, отколкото понятието определен интеграл, в XVII век. Когато Нютон и Лайбниц е създадена връзка между неразделна и диференциално смятане.

3.1. Проблемът на района на криволинеен трапец.
Изявление на проблема

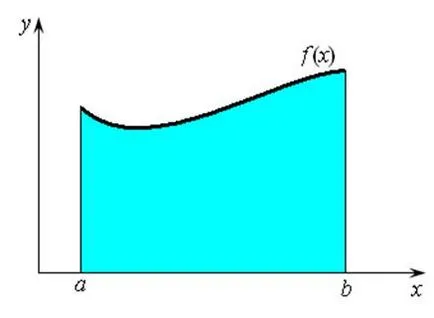
Помислете по-прост проблем, отколкото изчисления обем лимон: зоната на изчисление на криво трапец. Нека непрекъсната функция в интервал, който се намира над графиката Ox ос. Curve и прав и, както и Ox на ос. ограничават определен регион на равнината, наречен извита трапец (фиг. 3.1).

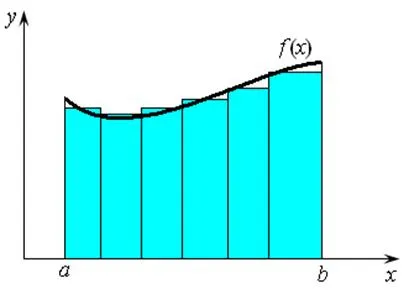
Площта на криволинеен трапец може да се изчисли с помощта на тънки правоъгълници. Лайбниц смята, че криволинейна трапец се състои от безкрайно тънки правоъгълници (фиг. 3.2). Всеки правоъгълник лежи над х сегмент точка и е с височина и ширина DX. Площта на този правоъгълник. Общата площ S е количеството пространство и е означен

По този начин, символът означава сбора от удължението се случи и букви S (лат. Сумата на думата).

Ясно е, че при изчисляването на площада е невъзможно да се управлява краен брой стъпки. Интуитивно, това се е чувствала древногръцките учени. Вярно е, че се опитват да избегнат безкрайните процеси. Още в V инча пр.н.е. Гръцкият философ Зенон Eleysky доведе редица парадокси, които възникват, когато или парадокси. Сред най-известните е апория "Ахил и костенурката", който гласи, както следва: Ахил, героят на Троянската война, няма да могат да се изравнят с костенурката. В действителност, докато Ахил ще продължи до разстоянието го отделя от костенурка, тя ще се премести някъде напред по пътя. След това, когато Ахил се преодолее разстоянието за пореден път се появи пред него, костенурката ще се премести напред отново, и т.н. Много учени са се опитвали да обяснят парадоксите на Зенон. Но нито един от предложените обяснения не може да се счита за напълно задоволителна. Очевидно е, че е невъзможно да се направи, тъй като парадоксите отразяват конфликта в реалния живот между отделно и непрекъснато, крайността и безкрайността.

Великолепната опит да избяга от безкрайност при изчисляването на мерките е методът на изтощение. проектирана от известния древногръцкия философ Eudoxus и плодотворно използва от много от сънародниците си, включително и Евклид и Архимед. Същността на метода на изтощение може да бъде обяснено със следния пример. При изчисляване на площта на кръг се счита за вписан и ограничена правилен многоъгълник с увеличаване на броя на страните, площта им се изчислява, а след това се приема като площта на площ кръг ограничи тези полигони.

Ясно е, че гърците не могат да направят това, те не знаят теорията на ограничения, толкова повече те са били по никакъв начин да се избегнат безкрайни количества. Архимед, например процедира, както следва. Той прекарва няколко последователни изчислителна гений усети по никакъв начин отговор, а след това стриктно (чрез индукция) твърди, че отговорът, който предположил правилно. В XVII век. броя на нерешените проблеми по този начин се е увеличил значително, но така единен алгоритъм създаден и не беше. За всяка задача изисква индивидуален подход. Едва през 70-те години на XVII век. Нютон и Лайбниц независимо Установено е, че алгоритъмът е създаден интегрално смятане.

Очевидно е, че в спора означаваше много български поет Bryusov, когато пише тези редове:

За Лайбниц, градински чай, създателят на пророческите книги!
Ти беше над света, като древните пророци.
Вашата възраст, чудейки се на вас, пророчество не е достигната
И ласкателство смесва безумни обвинения.

3.2. Определен интеграл като граница на интегралните суми

Да предположим, че F функция (X), определена от интервал. Тази дължина п е разделен от произволно, не непременно равни части: