Нормално уравнение на линия

В тази статия внимателно демонтирани нормалното уравнение на линия на самолета. Първо нормално уравнение уравнение получава линия е пример за нормална линия. По-нататък определя фактор нормализира и се разглоби да донесе общото уравнение на права линия към нормален изглед. В заключение, на примерите, показани в нормално уравнение Основното приложение на пряка - намиране на разстоянието от точка до линия на самолет.

Навигация в страниците.

Нормалната уравнението на линията - описание и пример.

Ние се извлече нормално уравнение на линията.

Нека равнината, определена правоъгълна Декартова координатна система Oxy. Ние определяме права линия в тази координатна система, като се посочва мястото, през които тя преминава, и нормалния вектор на линията. Като наш нормален вектор линия вземат единица вектор, започвайки от точката О. Неговите координати са равни, съответно, и къде - ъглите между вектора и положителните посоки Ox и Oy оси, съответно, т.е.. В точка, през която прави, вземе точка А, и се приеме, че той се намира на разстояние р единици () от точка O в положителната посока на вектор (р = 0 в точка А в основата), т.е..,.

Ние се получи уравнението, който определя правата линия.

Очевидно е, че точката се намира на разглеждания ред, ако и само ако цифровата проекцията на посоката на вектора е равен на стр. това е, при условие.

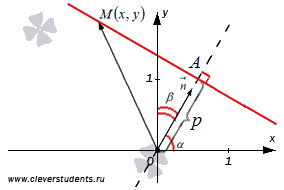
- радиус вектор на точка, следователно, е показано в координатите на точка на радиус вектор от точка. След определянето на скаларна продукт на вектори, ние получаваме равенството, и една и съща скаларна продукт в координатна форма е. Следователно, или. На този извод нормалното уравнение е завършена.

Получената уравнението е от вида, посочен като нормална уравнение или нормализираната линия уравнението на права линия. Уравнението се нарича уравнение на права линия в нормална форма.

Очевидно е, че нормалната уравнението на линията е общото уравнение на права тип, в която номерата А и В са такива, че дължината на вектор е един и номер C не е отрицателно.

От изхода на нормалното уравнение на права линия виждал геометричния му значение. нормално уравнение определя с права форма в правоъгълна координатна система Оху равнина нормална линия вектор на единица дължина намира на разстояние р единици от произхода в положителната посока на вектора.

Ето, например, нормално уравнение на права линия. Това Oxy в правоъгълна координатна система в равнината определя права линия, нормалната вектор от които има координати, и тази линия е отдалечен от произхода в 3 единица в посока, съвпадаща с нормалната посока на вектор.

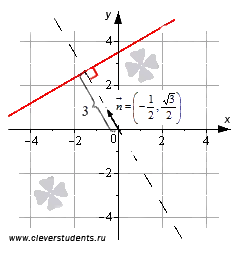
Намаляване на общото уравнение на права линия към нормален изглед.

Много често в този проблем, решаването на които включва използването на нормалното уравнение на права линия, права линия уравнение не е даден в нормална форма, както и във всяка друга. Ето защо не е ново предизвикателство: да донесе дадена линейно уравнение в нормален вид. Сега ние я имаме и ние ще се разбере.

Просто имайте предвид, че нормалната уравнението на линията може да бъде получена от общото уравнение на права линия. Ако по права линия на равнината, определена по друг начин да насочи в уравнението, това уравнение трябва първо да доведе до общо уравнение на линията. и след това е общо уравнение на линията към нормален изглед.

Така че, показват общото уравнение да донесе преки към нормалното уравнение права линия.

За да се доведе общият уравнението на линията към нормалния необходимостта да се размножават от двете страни на така наречената нормализиране фактор. който е равен. Нормализирането фактор знак обратна на знака на термина взети S. С = 0. Ако нормализиране знак фактор е без значение и може да бъде избран произволно.

Помислете за няколко примера за решения.

Дайте уравнение на линия в нормален изглед.

Ние са дадени общото уравнение на права линия, където к = 3. В = -4. С = -16. По този начин коефициентът на нормализиране трябва да се приема с "+", тъй като C - отрицателно число. Ние се изчисли стойността на коефициента на нормализирането на :. Умножете от една пета от двете страни на оригиналната уравнението. Последното равенство е нормално уравнение на дадената линия.