Монотонност на урока - 10 клас, Алгебра
Урок и представяне на алгебра в 10-та степен по този въпрос. "Характеристики на изследването в монотонността на проучвания Алгоритъм"
Какво ще да научите:
1. Намаляване и увеличаване на функции.
2. Съобщение производно и монотонност.
3. Две важни теореми на монотонност.
4. Примери.
Момчета, преди да са проучили няколко различни функции и техните графики. Сега нека да ви представим новите правила, които работят за всички функции, които сме разглеждат и ще бъдат допълнително разгледани.
Намаляване и увеличаване на функции
Нека да разгледаме идеята за увеличаване и намаляване на функции. Момчета, каква е функцията?
Функция е линия у = е (х), където всяка стойност на х се определя уникална стойност на у.
Нека да погледнем графиката на функция:
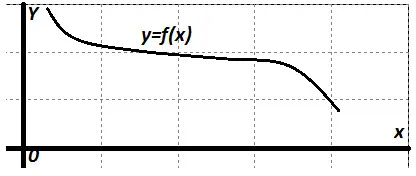
На нашите диаграма показва: колкото по-X, по-малката ш. Така че, нека да се определи намаляваща функция. Намаляване функция се нарича, ако по-голямата стойност на аргумента съответства на минималната стойност на функцията.
Ако х2> x1, тогава е (х2) x1, тогава е (х2> F (х1), или по-х, по-у.
Ако функцията се увеличава или намалява по някакъв интервал, тогава казваме, че е монотонно на този интервал.
Съобщение производно и монотонност
Момчета, но сега нека да мисля за това как да се прилага концепцията за производно в изследването на графики на функции. Начертайте графика за увеличаване на диференцируема функция и извършва няколко допирателни към нашия график.
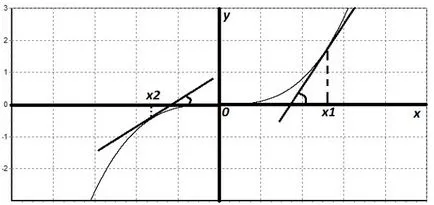
Ако се вгледате в нашите визуални допирателни или да притежават друга тангента, може да се види, че ъгълът между допирателната и положителната посока на оста х ще бъде остър. Следователно, тангента има положителен наклон. Наклонът на допирателната равна на стойността на производното на абсцисата точките на допиране. Така стойността на производната е положителна във всички точки на нашия график. За повишаване функция изпълнява следното неравенство: F '(х) ≥ 0 за всяка точка х.
Момчета, нека да погледнем графиката на функция намалява и изграждане на допирателната към графиката на функцията.
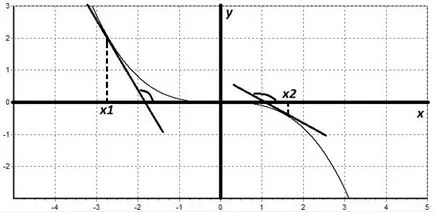
Нека да разгледаме допирателната и държите с ръка всяка друга допирателна. Отбелязваме, че ъгълът между допирателната и положителната посока на оста х - на тъп, и по този начин има отрицателен наклон допирателната. По този начин, отрицателна стойност на деривата във всички точки на нашия график. За намаляване функция изпълнява следното неравенство: F '(х) ≤ 0, за всяка точка х.
Така че, монотонността на функцията зависи от знака на производната:
Ако функцията се увеличава междината и е производно на този интервал, това производно не ще бъде отрицателно.
Ако функцията е намаляване на интервала и е производно на този интервал, това производно не е положителен.
Важно. интервалите, през които ние гледат на функцията бяха отворени!
Две важни теореми на монотонност
Теорема 1. Ако за всички точки на отворен интервал Х изпълнява на F неравенство '(х) ≥ 0 (където равенството на нула на производното, или не извършва или извършва, но само в ограничен набор от точки), като функция у = F (х) се увеличава интервала H.
Теорема 2. Ако цялата отворена разликата посочва X отговаря на неравенство F '(х) ≤ 0 (където равенството на нула на производното, или не извършва или извършва, но само в ограничен набор от точки), като функция у = F (х) намалява в интервала H.
Теорема 3. Ако всички отворения период на рентгеновите точки на равенството
F '(х) = 0, тогава функция у = F (х) е постоянна в този интервал.
Примери за проучвания функция в монотонността
1) За да се докаже, че функция у = х 7 + 3 х 5 + 2х - 1 се повишава до цялата реално линия.
Решение: Нека да се намери производната на нашата функция: у '= 07 юни + 15x 4 + 2. От степен, когато х е равен, тогава функцията мощност отнема само положителни стойности. Тогава у '> 0 за всяко от х, и по този начин, от Теорема 1, нашата функция се увеличава на цялата реална линия.
2) докаже, че функция намалява: у = грях (2х) - 3 пъти.
Нека да се намери производната на нашата функция: Y '= 2cos (2x) - 3.
Ние решаваме неравенството:
2cos (2х) - 3 ≤ 0,
2cos (2х) ≤ 3,
COS (2х) ≤ 3/2.
защото -1 ≤ COS (х) ≤ 1, така че нашата неравенството е изпълнено за всяко х, след това, от теорема 2, функция у = грях (2х) - 3x намалява.
3) Тест за монотонността на функцията: у = х 2 + 3 х - 1.
Решение: Нека да се намери производната на нашата функция: у '= 2x + 3.
Ние решаваме неравенството:
2x + 3 ≥ 0,
х ≥ -3/2.
Тогава функцията ни се увеличава с х ≥ -3/2 и намалява х ≤ -3/2.
Отговор: Ако х ≥ -3/2 - функция се увеличава, когато х ≤ -3/2 - функция намалява.
4) Тест за монотонността на функцията: у = $ \ SQRT $.
Решение: Нека да се намери производната на нашата функция: у '= $ \ Фрак> $.
Ние решаваме неравенството: $ \ Фрак> $ ≥ 0.
Нашата неравенството е по-голяма или равна на нула:
$ \ Sqrt $ ≥ 0,
3x - 1 ≥ 0
х ≥ 1/3.
Ние решаваме неравенството:
$ \ Фрак> $ ≤ 0,
$ \ Sqrt $ ≤ 0,
3x - 1 ≤ 0.
Но това е невъзможно, тъй като квадратен корен се определя само за положителни прояви, след периоди на спад в нашата функция там.
Отговор: ако х ≥ 1/3 функция увеличава.
Задачи за независим решение
а) За да се докаже, че функция у = х + 4x 3 9 + 1х - 10 се увеличава по цялата реално линия.
б) докаже, че функцията намалява: у = COS (5х) - 7х.
в) Тест за монотонността на функцията: у = 2 х 3 + 3x 2x + 5.
г) Тест за монотонността на функцията: у = $ \ Frac $.