Методът на крайните елементи в конструкцията

За решаване на физическите и инженерни проблеми в дизайна на многоетажни носещи конструкции в строителството бяха решили да използват числени методи. Един от най-често срещаните и ефективните от тях както в България и по света е метода на крайните елементи (МКЕ). Водещата позиция на този метод се дължи на широко пространство и относителната простота на употреба: независимостта на изчисляване на типа структура и физични свойства на използваните материали, опростени структури счетоводна система за сетълмент на взаимодействие със заобикалящата ги среда, способността да се автоматизират изчисленията на всеки етап.

Историята на метода на крайните елементи

Методът на крайните елементи в изграждането на първата практика е била използвана в началото на 50-те години на ХХ век. Първоначално, нейното развитие се наблюдава при две независими едно от друго направления: инженеринг и математика. В ранния етап на метод формулировка отблъснати само от принципите на структурните механика и значително ограничава обхвата на неговото прилагане. Едва след формулирането на основите на метода на крайните елементи с възможност за малки отклонения, станало възможно използването му в други задачи. Активното развитие на метода на крайните елементи и допринесе за постигане на напредък в областта на компютърните технологии, както и има възможност за използването му в повечето области на науката и практиката.

Етапи на развитието на метода:

1. При разработването на метода на крайните елементи са играе ролята им като вариационни принципи на механиката и математически методи, които се основават на вариационните принципи. Извънредни задачи по метода на Риц вариационен за първи път е използвана от Ричард Courant през 1943 г. и само в 50-те години на ХХ век са видели светлината на една и съща работа и от други учени (Poly, Хърш и други).

4. математическа теория на метода се появява само в 70-те години, неговият произход може да се проследи в трудовете на учени като I. баба, Р. Галахър, J. Dec-ЕД, J .. Оден, Г. Strang, J .. Fix. Значителен принос е направен и български учени. Например, V.G.Korneev сравнение математическата естеството на метод елемент и вариационен-разлика метода на крайните и имат съгласие. На същата тема е работил L.A.Rozin. А A.S.Saharovym Въртящ момент диаграма CE е разработен.

5. Последният път, особено през последното десетилетие се характеризира с бързо развитие и прилагане на метод на крайните елементи за изчисляване на структурните динамика, оптимизация на дизайна и отчитане нелинейно поведение.

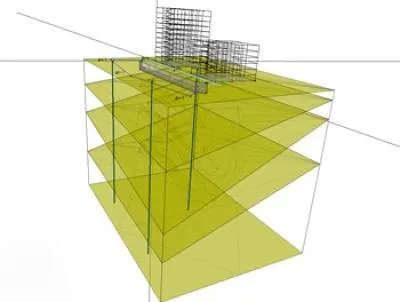
Същността на метода на крайните елементи

Преди извършване на анализ на конструкцията трябва да го представя във форма, разбираем за електронен мозък, т.е. компютър. И тъй като компютърът може да работи само с числа, а дизайнът трябва да бъде точно представена в цифров вид. Така, че е необходимо да се създаде математически модел, който не само ще отговарят напълно на изчисленото структура, но се състои само от цифри. Целта на работата ще бъде решение на този математически модел и определението на непознатото.

Същността на метода на крайните елементи е да се разделят на цялата площ, заета от структурата на няколко малки под зони с ограничен размер. Тези поддомейни се наричат ​​крайни елементи, както и себе си дял се нарича вземане на проби.

Форма крайните елементи ще зависят от вида на дизайна и характера на деформация. Например, крайните елементи на базата лъчеви структури (ферми, греди или кадри) ще бъдат части от пръти, при изчисляването на двуизмерни непрекъснати системи (вафли, плочи или черупки) - правоъгълни или триъгълни подобласти, и изчисляване на триизмерни структури (масиви или дебели плочи) - поддомейн под формата на паралелепипед или тетраедър. Но за разлика от настоящия проект по такъв дискретен модел на крайните елементи на свързването се извършва само в отделни възли (точки) в известен брой възли параметри.

Функционално енергия на цялата структура при вземане на проби е алгебричната сума на отделните функционални елементи на крайното, както и за всеки подрегион трябва да бъдат определени независимо от друга закона за разпределение, необходими за решаване на функции. С тези закони подвижно експресионни (желаните непрекъснати променливи) в рамките на предварително определен краен елемент чрез стойностите на крайните точки.

Броят на възли и броя на възможните премествания (степен на свобода) на крайния елемент може да бъде разнообразна, но по-малко от минималната сума, необходима за разглеждане условия под влияние на стреса на крайните елементи или напрежението в модела приет, те не трябва да бъде. Степента на свобода на краен елемент се определя от броя на независимите движения във всичките си сайтове. Степента на свобода на проектиране на цялата изчислява и, следователно, системи за алгебрични уравнения ще бъдат определени чрез сумиране на броя на измествания на всички известни сайтове. Въз основа на факта, че основната неизвестното в метода на изчисление на изместването - неизвестните възлови премествания, степента на свобода на концепцията за крайни елементи и конструкции изцяло стане особено важно в метода на крайните елементи.

Метод за вземане на проби разглеждания район, броят на крайните елементи, броят на степените на свобода и формата на приблизителни функции използват, има пряко влияние върху точността на изчисление на събранието. По този начин, метода на крайните елементи за най-алгебрични, не само помага при изчисляването на някои строителни конструкции, но и като цяло в проблемите със строителството.

Пример за изчисляване на непрекъснати двуизмерни структури

Да разгледаме пример на двумерен изчисляване на траекторията структури (вафли или плаки) по метода на крайните елементи, която се състои в извършване на следните стъпки:

1. Изследваният региона компрометирана използвайки мрежата е разделен на определен брой елементи, които се очаква да бъдат свързани помежду си, в резултат на окончателния размер на възлови точки, които са разположени в границите на елементите. Неизвестни параметри проблем трябва да се реши, а ще свирят генерализирано движение на тези възлови точки, а броят им ще бъдат неразривно свързани с известен брой на степените на свобода.
2. Входна функция за характеристики на генерализирани премествания, които ще определят разпределението на всеки един от елементите на генерализирана изместване на възлови точки. Също така, тези функции ще определят полето на деформация и на усилията в рамките на елементите, както и по границите, както добре.
3. Тя извършва строителството на матрица скованост основава на принципа на допустимото изместване. Матрицата трябва да балансира разпределя натоварването и усилията на границите на елементите води чрез обобщени премествания възлови точки.
4. Създадена скованост матрица на цялата структура на основата на коравина матрици на отделните елементи. Този етап се свежда до решаване на получената система от уравнения в който избраните параметри на базата на изместване на възлови точки, определени от състоянието на цялата сграда структура по отношение на щам и стрес проста алгебрична.