метод почистване

Освен това, с помощта на уравнения (1.7) и progonochnyh коефициенти на изразите (1.8) и (1.9) последователно се изчисли Xn-1. Xn-2. x1.

При изпълнението на метода за почистване е необходимо да се помисли, че при спазване

или най-малко един двупосочен има строго неравенство (1.12), разграничението между "0" се заличават, а системата има уникално решение.

Имайте предвид, че условието (1.12) е достатъчно, но не е необходимо. В някои случаи, добре кондиционирани системи (1,7) метод на почистване може да бъде стабилен и неспазване състояние (1.12).

Схема метод почистване алгоритъм може да има формата, показан на Фигура 1.2.

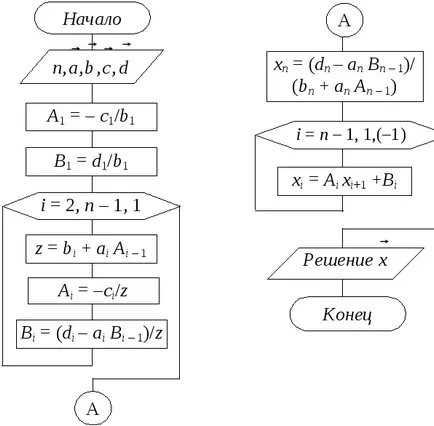
Фигура 1.2 - блок-схема на метод за почистване

Итеративен методи за решаване Slough

Предимството на итерационни методи е тяхната приложимост към болни с климатик системи и системи с голяма поръчка, samoispravlyaemost и лесен за изпълнение на компютър. Итерационни методи за изчисляване началото на работата изискват първоначално приближение до желаното решение.

Трябва да се отбележи, че условията и степента на сближаване на процеса на повторение силно зависят от свойствата на матрична система от А и на избора на начални приближения.

За да се приложи методът на повторения на оригиналната система трябва да бъдат доведени до повтарящ ума

и след това извършване на итеративния процес от формули повторение:

матрица G и вектор

получен чрез превръщане на първоначалната система.

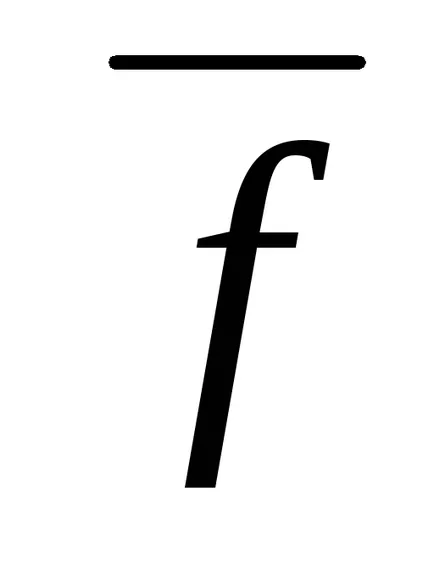
За засилване на сближаването на метода (1.13 *) е необходимо и достатъчно условие | i (G) | <1, где i (G ) — все собственные значения матрицы G. Сходимость будет и в случае, если ||G || <1, ибо |i (G )| < ||G || ( — любой).

Символът ||. || Тя е в норма на матрицата. При определяне на стойността му често се спре да се провери две условия:

|| G || =

или || G || = , (1.14)

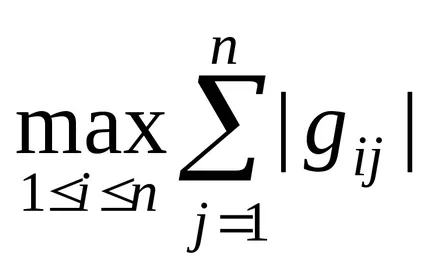
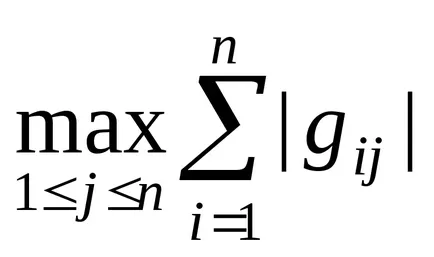
където

. Сближаване е гарантирана също така, ако източникът е matritsaA диагонално доминиращ, т.е.. Д.

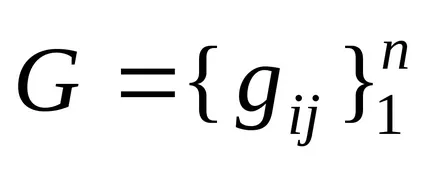
Когато условията (1.14) или (1,15) е изпълнено, методът итерация клони за всяка първоначална сближаване

. Най-често векторили да вземе нула или единица, или самият векторот системата (1.13).

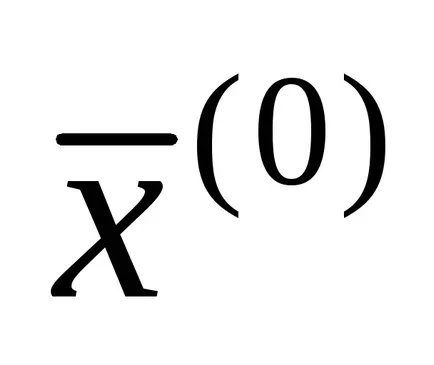
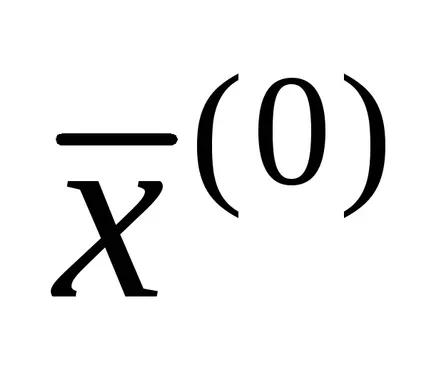
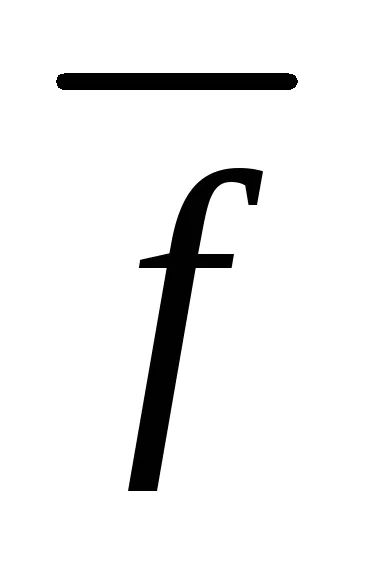
Ако състоянието (1.15), след това превръщане на итеративен форма (1.13) може да се осъществи просто чрез решаване на всеки и-ти уравнение на системата (1) по отношение на XI в следните рецидив формули:

Ако матрицата не е диагонал господство, тя трябва да бъде постигната чрез някой от неговите линейни трансформации, които не нарушават тяхната равностойност.