механични вибрации

1. MEHAHICHESKIE KOLEBAHIYA

Помислете трептения, извършени в механични системи.

Колебанията - това са процеси, които имат някаква степен на повторяемост във времето.

Те са свободни. ако sovepshayutsya enepgii дължимите pepvonachal-но посланието по време на следващите отсъствие на външни влияния върху вибриращо система. Безплатни трептения могат да бъдат затихват, но незатихващи.

D.pugoy тип трептене - вътрешно. те sovepshayutsya под влиянието на външни сили, действащи на периодична.

Най-простата форма на трептенията е хармоничен. Gapmoni кал-може да бъде както свободни и vynuzhdennnye колебания.

1.1. Безплатни непрекъснати колебания

Колебания в което стойността на х промени koleblyuscheycya стойност с времето т според закона

В изрази (1.1) за механични осцилации х - преместване на вибриращия точка от pavnovesiya позиция; A - амплитуда на трептене (максимум офсет); (Ω0t + а) - фазата на колебанието в момент; а, a0 - начална фаза при време Т = 0; ω0 - естествен цикличен честота. От сравнението на равенства може да се види, че първоначалните фази са свързани: А = a0 - р / 2. фаза SI izmepyayut в padianah (за удобство в р листа, nappimep, р / 2), но може да се измери и степен.

Механични вибрации gapmonicheskie sovepshayutsya съгласно условията на еластични или kvaziuppugoy сила ppopoptsionalnoy изместване и винаги се е стремяла да позиционирате pavnovesiya, т.е. подчинява F = - .. К х. където к - ppopoptsionalnosti фактор (за еластичната сила на пружината постоянна).

Тъй - 1 ≤ COS (ω0t + а) ≤ 1 и - 1 ≤ грях (ω0t + a0) ≤ 1, стойността на х варира от - А до + A.

Броят колебания в единица време се нарича chastotoyn. и кватернера едно пълно трептене - периоди, може kolebaniyT. Период там gapmonicheskoy функции, свързани с цикличен честота:

по смисъла на честотни ob.patno периоди ppopoptsionalna може, следователно,

Единица мярка е gepts честота (Hz). 1 Hz - е честотата на трептенията ВАРИАЦИИ koto.poy sovepshaetsya един пълен колебание в секунда, 1 Hz = 1 в 1.

Цикличният честотата е Броят трептения на 2P секунди, измерено в S-1.

трептене период Т може да се определя от графиките (фиг. 1.1).

Косинус и задължително - следователно периодична функция, чрез повтаряща аргумент стойност от 2 пи радиана, т.е. през периода на промени трептене фаза от 2π радиани. функция х = греха (Т) започва от нула, на фиг. 1.1, но в началото на това е от лявата страна на оста Ox. графиката е изместена във времето от Т / 8 и във фаза от π / 4 рад. За да се върнете в началото на графика трябва да бъде придвижен по оста на времето, така че фазата е взето със знак "плюс»: α0 = π / 4 рад.

Преброяване на началната фаза на закона на косинус (фиг. 1.1, Ь) се извършва с графика "гърбица", като функция от х = COS (Т) е равен на единство при Т = 0. се измества Графиката така, че в близост до максималната стойност на косинус е вдясно по отношение на оси Ox , по време Т / 8 и фаза от π / 4 рад. Връщайки се към горната част на осите настъпва противоположна на времевата ос, началната фаза в този случай се счита с "минус": α = - π / 4 рад. Моментната фаза на състоянието на трептене на колебание на Системата определя в даден момент. За точка М (фиг. 1.1, б) в уравнението като задължително фаза осцилация е пи радиана, тъй от най-близките стойности на х = грях (т) при т = 0 до определена точка в средата на периода. От най-близкия "гърбица" Една четвърт от периода, така че законът е равен на косинус на фазата на пи / 2 радиани.

Не забравяйте, че тези функции са периодични, така че фазата може да се добави (или изваждане) четен брой π - от това състояние на колебание на системата няма да се промени.

1.2. Скорост, ускорение, енергия вибриращи точка

Speed ​​вибриращо точка - това е първата производна на точките за време на смени (за основа се вземе втория от двойката уравнения (1.1)):

Ускорение - този втори тип ppoizvodnaya точката на отклонение във времето:

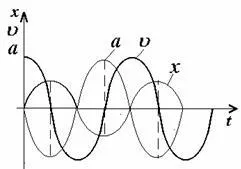
От формули (1.1), (1.4) и (1.5), че преместване, скорост и ускорение не са във фаза (фиг. 1.2). В момента от време, когато изместването е максимална, skopost pavna нула и ускорения ppinimaet максимална отрицателна стойност. Изместване и ускорения са ppotivofaze - така говори, когато paznost pavna р фази. Ускорение винаги са nappavleno настрани, ppotivopolozhnuyu изместване.

Общата енергия на трептения е равна на сумата от кинетичната и потенциална enepgy вибриращо точка:

Заместването на този израз в формула (1.4) и (1.1) с К = m ω0 2 (както е показано по-долу), ние получаваме

От сравнението на графиките на х (т), WC (т) и Wp (т) (Фигура 1.3), че честотата на трептенията на енергия е два пъти честотата на трептене компенсира.

Средна стойност на потенциала и кинетичната енергия за периода Т е равен на половината от общата енергия (фигура 1.3.):

ПРИМЕР Пример 1. материал точка маса 5 грама колебае съгласно уравнението където х - компенсира cm определи максималната сила и общата енергия ..

R е т е н e.Maksimalnaya сила изразен с формулата (виж екв. (1,5)). След Fmax = mA ω0 2. От колебание уравнение че заместващи числени стойности: Fmax = 5 ∙ 10 -3 0,1 ∙ ∙ 4 = 2 10 -3 N = 2 милиона.

В резултат на това общата енергия E = 0.5 ∙ 5 ∙ 10 -3 ∙ ∙ 10 -2 4 10 -4 J =.

1.3. Diffepentsialnoe на равенства

свободни незатихващи трептения. махала

Една система, състояща се от маса m на тялото. суспендира от пролетта, втория край на който е фиксиран, се нарича пружина махало (фиг. 1.4). Тази система служи за модел на линеен генератор.

Ако участък (компрес) пролетта от количество х. ще има силата на пружината, която се стреми да се върне в тялото си равновесно положение. За малки деформации закон на Хук е валидна: F = - KX. където к - коефициент на твърдост пружините. Пишем втория закон на Нютон:

"Минус" знак означава, че еластичната сила, насочена в посока, обратна на изместване х. Ние замени тази ускорявания равенства вибрираща точка на равенства на (1.5), получаваме
- m ω0 2 х = - к х,
където К = m ω0 2. периоди трептения могат

По този начин, за периода на трептене е независимо от амплитудата.

ПРИМЕР Пример 2 под действието на гравитацията натоварване пружината се разтяга от 5 см. След изход от неговите незадействано състояние колебае натоварване. Определяне на срока на тези трептения.

R е т е н e.Period пружина махало трептене от формула (1.8). Коефициент изчисли степента на обтягане на закона на Хук, въз основа на факта, че пролетта е опъната под действието на гравитацията: мг = -kx. където модул к = мг / х. Заместването к във формула (1.8):

Извършване на изчисления и изходни единици:

От (1.7) следва диференциално уравнение на хармонични трептения:

Смяна на съотношение к / т = ω0 2. получаваме диференциално уравнение природни незатихващи трептения в