Математически безнадеждни хуманитарни науки

Ние се състезава за Cheshire Cat и спада на многоизмерно пространство.

Представяме Ви към следващия урок от професор по приложна математика Нели Литовския, което, заедно с журналиста Алла Kechedzhan реши да реабилитира изплашените ПМГ хуманитарните науки. За да направите това, Нели и Алла организирана група във Фейсбук за всички "Математика - най-голямата и страшна."

Сайтът Newtonew Нели всяка седмица разделен материал премина към групата. Това са линкове към предишните уроци, така че да не пропуснете нещо:

Ура, интеграли се правят! Ние се уверете, че питагорова теорема ни дава възможност да се изчисли разстоянието не само по права линия, а крива.

Какво става, ако не сме в самолета и в триизмерното пространство? В крайна сметка, нашият свят не е плоска, като триизмерен!

А разстоянието по права линия в триизмерното пространство, може да се изчисли отново на питагорова теорема. Нека се опитаме да го направим.

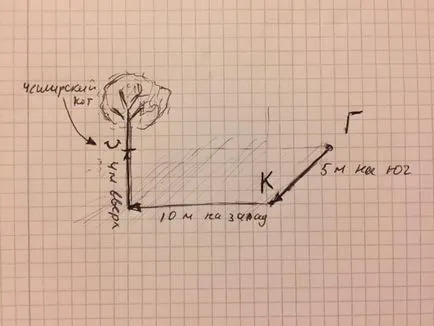
Работа. Cheshire Cat бяга от херцогинята (T). Той е свършила 5 метра на юг. Но по пътя си подстригана Queen (K) и е на път да крещи: "Off с главата си" Хитър Cat наведе и се затича на запад, на 10 метра до най-близкото дърво. Дърво котка се изкачи до 4 метра.

Въпрос: Какво е разстоянието (в метри) по права линия от херцогинята на Кота? (Тъй като това е най-Cheshire Cat, той, разбира се, са изчезнали, една усмивка ляво на фигурата).

НАЙ-ВАЖНО: Това е само достатъчно отговор. Обяснете непременно като вярвал!

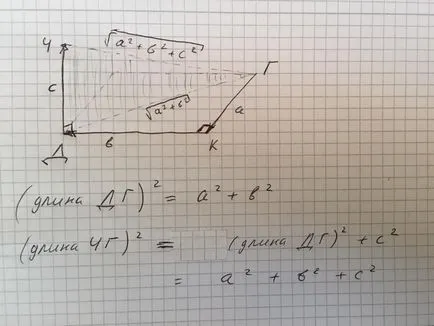
два триъгълника да виждат: 1 - "лежи" GCD (Duchess - Queen - дърво) и 2 - "стенд-нагоре" GDCH (Дукеса - дърво - Cheshire Cat). Ако успее, то е ясно, че ГД крак - е хипотенузата на първия триъгълник лежи ГРУ. Знаейки, дължината на двата крака на премиера и Държавната Дума, според питагорова теорема, ние откриваме, дължината на хипотенузата на МС. Единственият проблем е, дължината на крака хипотенузата ГД. DG = корен на сбора от квадратите 5 и 10 = 25 + 100 = А (която не е равна помни, че 2 ^ 11 = 121, тогава GD е 11 m и Troshka cm). Сега MS. Това корен (16 + GD ^ 2) = SQRT (16+ (5 ^ 2 + 10 ^ 2)) = 11,87434209.

Между дървото и ъгъла на земята очевидно е права линия. Един от крака си - разстоянието от основата на дървото, за да Кота - 4 метра, а вторият - от основата на дървото на кралицата - 10 метра. Следователно, от теоремата на Питагор хипотенузата на дължина - разстоянието от Кота да spugnuvshey му кралица. Ние вярваме: SQRT (4 ^ 2 + 10 ^ 2) = sqrt116. Сега знаем, че два крака в още един правоъгълен триъгълник, където хипотенузата - това е разстоянието между херцогинята и Котарака в права линия. Един от крака му - това е първият поход котката от любовницата си в Южна 5 метра на, а вторият - разстоянието между кралицата и котка, която току-що изчислява: SQRT (116 + 5 ^ 2) = 11, 87

Защо е важно да се знае посоката на движение на котката - първо на юг, а след това на Запад? За да не се губят в пространството на прав ъгъл!

Между другото, някои преводачи Карол е бил убеден, че е котка Cheshire. На английски език и в действителност котката, а котката - само "котка".

Хоризонталната равнина на траекторията на план на котка - е краката на правоъгълен триъгълник. Права линия от D на основата на дървото - е хипотенузата на тази теорема на Питагор удовлетвори: корен квадратен от 5 ^ 2 + 10 ^ 2 = 125. Корен квадратен от 125 е 11.2. Вертикална (дърво) котка летял до 4 м. И това вертикално разстояние с открит дължината на хипотенузата отново прилича крака на правоъгълен триъгълник, дължината на хипотенузата на което е най-желаното разстояние. 4 ^ 2 + 11,2 ^ 2 = 16 + 125 = 141. Корен квадратен от 141 е 11.9. Отговор: 11.9 m.

На Фигура 2, задачата в повече схематична форма. Разстояние посочено на юг, запад и до писмата на. б. в. Точка е все още T (Дукеса), К (Queen), D (подножието на дървото) и В (Cheshire Cat).

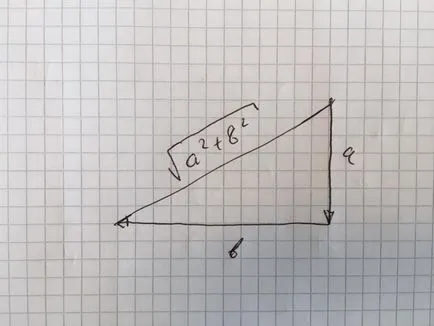
Ако отидете със самолет и м на юг и запад б, разстоянието по права линия е SQRT (а ^ 2 + б ^ 2), като питагорова теорема, виж фиг. 3. Оказва се, че ако добавите трета координира и мине метър нагоре, формула е много подобна, само увеличава третото измерение, а разстоянието е SQRT (а ^ 2 + б ^ 2 + C ^ 2).

Някои участници не бяха разгледани от питагорова теорема, и гледаха в интернет. Ако отидете на връзката. ще видите, че това разстояние се измерва в така наречената "евклидовата" пространство.

Евклидово пространство - това е най-общото пространство, което виждаме около нас. Разстоянието в това пространство, ние разбираме, "резултатите от измерването владетел." И това разстояние се изчислява с помощта на Питагоровата теорема.

Последната задача на една дълга поредица за питагорова теорема. В края на поглед към многомерен пространство. Multi-мерно пространство на въображението най-малко, защото те са почти невъзможно да си представим! Нашият мозък не знае как да се направи четири измерения на изображението, а само около десет или stomernyh и да кажа нищо.

Но защо тогава те трябва? Оказва се, че многоизмерното пространство е съвсем реална! Да започнем с това, представете си, че искаме да се напише функция, както е показано на фигура 4. коефициентите а. б. в. г могат да бъдат всякакви номера, т.е., ние имаме четири "степени на свобода". Оказва се, че такива функции, както е показано на Фигура 4, "на живо" в четири тримерно пространство.

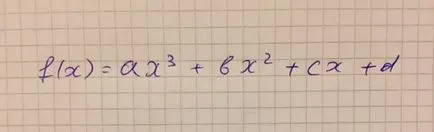
Получават Multi-тримерно пространство, когато ние описваме обект с помощта на няколко параметри. Например: възраст, височина, тегло, телесна температура. На второ място, ние сме в четириизмерното пространство!

Модерен онлайн свят е просто гъмжи пространства плашещи размери.

И параметрите на потребителите още по-: на броя на посещенията на всеки сайт, оценката на всеки елемент, за всяка заявка за търсене. има милиони възможности. Не е случайно, една от основните изчислителни задачи в системите за онлайн препоръка - е да се намали размерите.

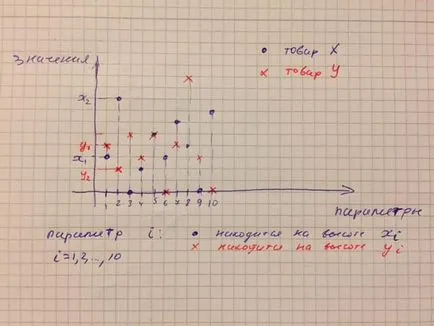
Работа. Онлайн магазин продава продукти. За простота, нека приемем, че стоките 10 параметри.

На Фигура 5, хоризонталната ос - номер на параметър. На вертикалната ос - стойността на стоката. В момента има 2 продукт: X (сини кръгчета) и V (червени кръстове). Параметърът стойности 1.2. 10 за продукт X ще бъде означен X1, X2. x10. и за американските стоки, съответно, U1. v2. U10.

Ние искаме да предложим на клиентите продукти, които са "подобни" на тези, които вече са закупени. Как да го направя?

ВЪПРОС: Има как да се разчита на "разстоянието" между двата продукта. Необходимо е, че разстоянието между "много различни" стоката е била висока, но между "подобни" продукти - малък.