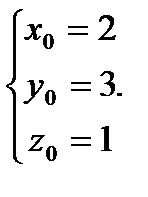линия уравнение направо в космоса - studopediya
В пространството директно а. минаваща през точка, успоредна на вектор. наречен употреба и директно вектор (фигура 14).
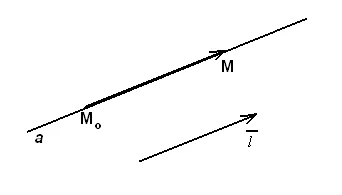
Нека точката - точката на постоянен ток. Vector се намира на прави и лежат на една права с. От състоянието на колинеарност на два вектора, ние имаме:
Тези уравнения - каноничните уравнения на права линия в пространството.
Ако каноничните уравнения за въвеждане на параметър т:. Ние се получи на параметричните уравнения на реда:
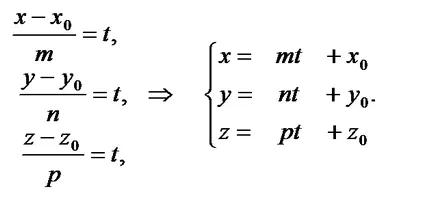
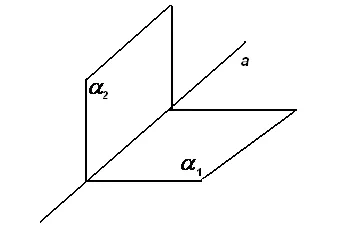
Линия може да се дефинира като пресечната точка на две равнини (фигура 15):
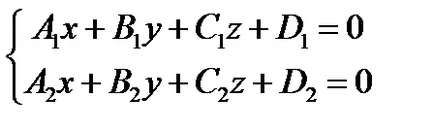
линия уравнение права, минаваща през двете точки и.
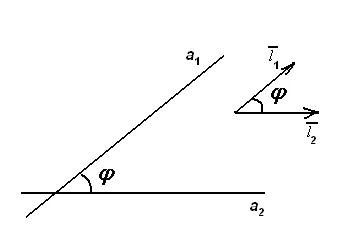
Ъгълът между редовете е равна на остър ъгъл между тяхната посока вектори (16 е) и се изчислява по формулата:
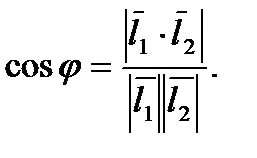
Пример. Директни поставените общи уравнения
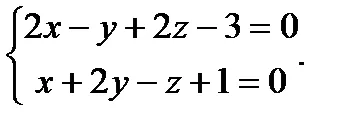
а) Напишете тази линия за канонични и параметричните уравнения;
б) Да се намери ъгъла между правата линия и правата линия, дадена от уравненията
а) Изберете една от точките, през които преминават посочената линия, определена от пресечната точка на самолети. Първоначалната система има безкраен брой решения, едно от които са получили една от променливите дават конкретна стойност. Да. След това стойностите на други неизвестни са открити от системата
Решението на тази система е един чифт от числа.
В резултат на това, ние получаваме най-важното. чрез който желаната линия. Като пример можете да вземете директен вектор вектор. къде. - нормалните вектори на равнини, пресичащи линия, която е права линия. По този начин,
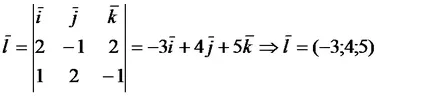
Нека пишат каноничните уравнения на права линия.
Ние получи от каноничните параметричните уравнения на права линия:
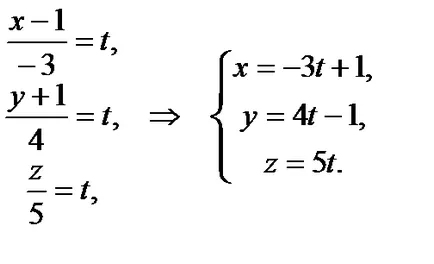
б) вектор посока на линията. посока вектор на прав ъгъл между редовете и е равна на остър ъгъл между тяхната посока вектори:
Ъгълът между правата линия и равнината
Да предположим, че са дадени права и равнина (Фигура 17):
Директно в посока вектор
Самолетът с нормален вектор
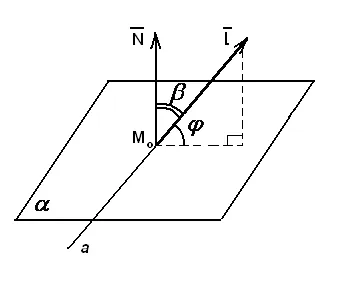
Ъгълът между правата линия и равнина, се изчислява по формулата:
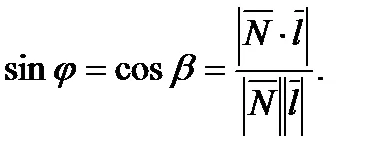
За да намерите точката на пресичане на линия и равнина. Ние трябва да насочим параметричните уравнения
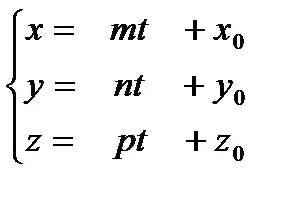
Пример. Намерете а) ъгълът между правата линия и равнината;
б) в точката на пресичане на линия и равнина.
.
Решение. - перпендикулярна на равнината; - посоката вектора на линията.
б) да замени на параметричните уравнения на права линия
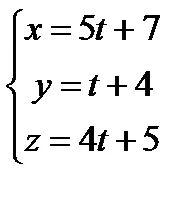
. - определяне на точката на пресичане на линия и равнина.
Ние замени стойността на параметъра в параметричните уравнения, получаваме: