линейното програмиране
x1. x2. Xn - входни променливи, Xn + 1. Xn + 2. Xn + m - допълнителни променливи. Всички допълнителни променливи, които сме поели като основа. и изходни променливи като nonbasic (допълнително записани в първата колона на таблицата и симплекс започване на първия ред). При всяко повторение на елементи на масата симплекс преизчисляват в съответствие с определени правила.
Симплекс метод алгоритъм.
Тук е проблемът на LP за канонична форма
В случай, че първоначалният проблем трябва да се намери най-малкото - знаците на коефициентите на целевата функция F са обърнати a0, п = -a0, п. Табели ограничения коефициенти на знак "≥" просто обърнати. Ако състоянието съдържа знака "≤" - коефициенти са написани непроменени.
Етап 0. образуват жива картина на симплекс, съответстващ на първоначалното проблема
Стъпка 1. Проверка за валидност.
Проверка на положителните елементи на колона B (постоянни семестъра), ако никой от тях не е отрицателен тогава ние открихме осъществимо решение (решение, съответстващо на един от върховете на условията полиедъра), а ние преминете към стъпка 2. Ако са налице отрицателни елементи в колоната от членовете да избирате сред тях най-много модул - тя определя водеща низ к. Тази линия също намери максималния модул отрицателен елемент ак, л - тя определя водещата колона - л и е водещ член. Променлива съответстваща на водещ ред се изключва от основа, съответната променлива е включен в основата водеща колона. Преизчисляване на масата за симплекс в съответствие с правилата.
Ако има отрицателни елементи сред свободните членове - и в съответния ред - в него няма условия за проблема са несъвместими, и тя все още няма решения.
Ако след преизчисляване на свободните членове на колоната остава otritsaetelnye елементи, се пристъпва към първата стъпка, ако няма такива, а след това на втория.
Стъпка 2: Проверка за оптималност.
В предишния етап ние открихме осъществимо решение. Проверете за оптималност Ако сред елементите на nahodschihsya на маса симплекс в ред F (без да се взема под внимание елемент B0 - текущата стойност на целевата функция) не е отрицателен, тогава ние открихме, оптималното решение.
Ако линията F, има отрицателни елементи на разтвора трябва да се подобри. Изборът между отрицателни елементи на F линията на максималния модул (с изключение на стойността на функцията B0)
л - колона, в която той е да бъде лидер. С цел да се намери олово линия, намери съотношението на съответния свободен член и член на водещата колона, при условие че те не са отрицателни.
к - редове, за които това съотношение е минимално - водещ. ак елемент, л - Водещ (позволява). Променлива съответстваща на водещата линия (ХК) се изключва от основа на променливата съответстващ на колона (XI) е включен в основата.
Преизчисляваме формули на масата симплекс. Ако отрицателни елементи остават в новата таблица за разпределение след скандал F преминете към стъпка 2
Ако не можете да намерите на олово линия, тъй като няма положителни елементи в колоната водещ в областта на изпълними решения на функцията за проблем не се ограничава до - алгоритъмът спира.
Ако линията F в колоната на членовете на всички елементи са положителни, тогава ние открихме, оптималното решение.
правила за преобразуване симплекс таблица.
При съставянето на новата маса симплекс в него следните промени настъпват:
- Вместо това, основната променлива XK запис XL; вместо nonbasic променливи XL напиши XK.
- задвижващият елемент се заменя с реципрочната стойност на ак, L '= 1 / ак, л
- всички елементи, водещи колона (с изключение на К, L), умножена по -1 / К, L
- всички елементи, водещи ред (с изключение на К, L), умножена по 1 / ак, л
- Останалите елементи симплекс маса се преобразуват от формула AI, J '= AI, J - AI, L х AK, J / ак, л
Схема преобразуване елементи симплекс маса (с изключение на водещ ред и колона резултата) схема, наречена "правоъгълник".
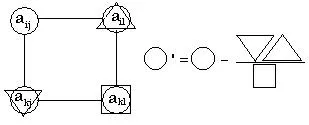
Convertible елемент AI, й и съответните три фактора са само върха на "правоъгълник".