Линейно уравнение, и примери с формула

Общ вид на линейно уравнение с едно неизвестно, както и на принципа на неговите решения

Всяко уравнение, което може да доведе до такъв вид запис:

Тя се нарича линейна. Това е обща формула. Но често в стремежа линейни уравнения, написани на неявна форма. След това, което искате да извършите еднакви трансформации, за да получите най-конвенционален записа. Тези действия включват:

Разкриване на скоби;
преместите всички условия с променливата в лявата ръка, а останалите - в дясно;
намаляване на сходни условия.

В случаите, когато неизвестен количество в знаменателя на фракцията, че е необходимо да се определи стойността, в която изразът няма смисъл. С други думи, се приема, да знаете областта на уравнението.

Принципът, на който се решават всички линейни уравнения, се свежда до, да споделят стойността на дясната страна на уравнението с коефициента пред променливата. Това означава, че "х" е равно на / а.

Специални случаи на линейни уравнения и техните решения

По време на аргументи могат да възникнат такива моменти, когато линейни уравнения, предприемат една от дадения вид. Всеки от тях има конкретно решение.

В първата ситуация:

Решения на това уравнение винаги ще бъде х = 0.

Във втория случай, "а" отнема на стойност, равна на нула:

Отговорът на това уравнение ще бъде произволен брой. Това означава, че има безкраен брой корени.

Третият ситуацията е както следва:

Това уравнение няма смисъл. Тъй като корените на това удовлетворяване, не съществува.

Общата форма на линейни уравнения в две променливи

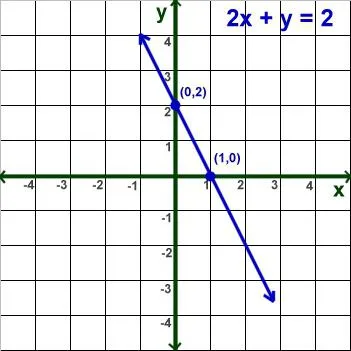
От името му, е ясно, че неизвестните в него за двама. Линейни уравнения с две променливи изглеждат така:

От записа има две неизвестни, отговорът ще се появи като двойка числа. Това не е достатъчно, за да се уточни само една стойност. Това е непълен отговор. Двойка стойности, за които уравнението става идентичност, е разтвор. И винаги пиша първата променлива в отговора, който идва по-рано в азбуката. Понякога се казва, че тези номера го удовлетворяват. Освен това, такива двойки могат да бъдат безкраен брой.

Как да решим линейното уравнение с две неизвестни?

За да направите това, просто вземете някоя двойка числа, които биха били верни. За простота, можете да вземете един от най-неизвестните е равен на който и да е просто число, а след това се намери втория.

Когато решението, често е необходимо да предприема действия за опростяване на уравнението. Те се наричат трансформации за самоличност. И за уравнения винаги притежават следните качества:

всеки термин може да бъде прехвърлена към противоположната страна на уравнението и да го замени с обратен знак;
лява и дясна страни на всяко уравнение е позволено да бъде разделена на един и същ номер, ако не е нула.

Примери за задачи с линейни уравнения

Първата задача. За решаване на линейното уравнение: 4 = 20, 8 (х - 1) 2 + 2 = (4 - 2); (5х + 15) / (х + 4) = 4; (5х + 15) / (х + 3) = 4.

В уравнението, което е на първо място в списъка, просто изпълнява подразделение от 4. В резултат на 20 е равно на 5. Това е отговор х = 5.

Третото уравнение изисква трансформация на идентичност е завършена. Тя ще бъде в разкриването на скобите и събирането на подобни термини. След първото действие на уравнението става: 8x - 8 + 2 = 8-4. След това е необходимо да се движат всички неизвестни в лявата ръка, а останалата част - в дясно. Уравнението ще изглежда така: 8x + 2x + 4 = 8 + 8 След привеждане тези термини: 14ч = 16. Сега, това изглежда по същия начин, както и първия, и решението му е лесно. Отговорът е х = 8/7. Но математиката се предполага да се разпределят цялата част на неадекватно фракция. Тогава резултатът ще се трансформира, и "х" е равно на едно цяло и една седма.

В други примери, променливите са в знаменателя. Това означава, че първо трябва да разберете за какви стойности на уравнението са определени. За да направите това, трябва да се отстранят на броя, в който знаменателите изчезват. В първия пример е "-4", а втората е "-3". Това означава, че тези стойности следва да бъдат изключени от отговора. След това трябва да се размножават и двете страни по проявата в знаменателя.

Премахване на скобите и привеждане тези условия, в първия от тези уравнения се получава: 5x + 4 + 15 = 16, и втори 5x + 15 + 4 = 12. Тъй като първото уравнение за тази трансформация е х = 1. Вторият е равно на "-3", което означава, че окончателните решения не е така.

Втората задача. За решаване на уравнение: -7Н + 2у = 5.

Да предположим, че първият неизвестното х = 1, то уравнението става -7 * 1 + 2y = 5. Чрез изместване на дясната страна на фактора "-7" и да го промените на знак плюс, можете да получите, че 2y = 12. Това означава, че = 6. Отговор: Едно от решенията на уравнение х = 1, у = 6.

Общата форма на неравенство с една променлива

са представени всички възможни ситуации за неравенствата тук:

Като цяло, тя изглежда като проста линейна уравнение, само знака за равенство се заменя с неравенството.

Условия за самоличност преобразувания на неравенството

Както и линейни уравнения и неравенства могат да бъдат променени в съответствие с определени закони. Те са, както следва:

за лявата и дясната страна, можете да добавите всякакви азбучен или числов израз, знак за неравенство ще останат същите;
също могат да бъдат умножени или дели на същата положителна броя от този знак не се променя отново;
когато се умножава или дели на същата негативна брой остава верен на половете при условие, промените знака за неравенство е наопаки.

Общ изглед от двойно неравенство

Проблемите могат да бъдат представени, такива неравенства изпълнения:

Удвоете той се нарича, защото ограничени признаци на неравенство и от двете страни. То се решава от същите правила като редовен неравенство. И намери отговорът се свежда до серия от трансформации за самоличност. До една проста.

Решение Характеристики двойно неравенство

Първият от тях е имиджа си по оста на координатната. Използвайте този метод за прости неравенството не е необходимо. Но по-тежки случаи може да се наложи само.

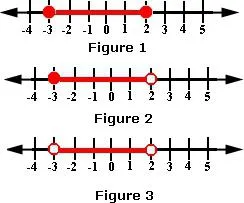
За изображения на неравенството трябва да се отбележи по оста на всички точки, които се получават по време на дискусиите. Този невалидни стойности, които са обозначени с пробиви и стойностите на неравенството, ние получаваме след трансформация. Тук също, че е важно да се направи точка. Ако строго неравенство, т.е. <или>, тези стойности са пробити. В не-строги неравенството по отношение трябва да се боя.

След това би трябвало да се определят смисъла на неравенството. Това може да стане чрез люк или дъги. Тяхната пресечната ще покаже отговора.

Втората особеност е свързана с неговата сметка. Той предлага две възможности. Първо - това е последната неравенство. Вторият - под формата на време. Ето с това е, че има трудности. Отговор интервали винаги изглежда като променлива със знака на аксесоари и скоби с номера. Понякога получава малко интервали, а между скобите, което трябва да се напише на характера "I". Тези знаци са, както следва: ∈ и ∩. Пропуски в скоби също играят роля. Кръгла сложи когато точката е изключен от отговора и включва правоъгълна стойност. Infinity знак е винаги в скоби.

Примери за разтвори на неравенства

1. решаване неравенството 7 - ≥ 5х 37.

След прости трансформации получени: -5Н ≥ 30. Разделяне с "-5" може да се получи експресия: х ≤ -6. Това е отговорът, но тя може да бъде написана по различен начин: х ∈ (-∞; -6].

2. решаване на двойно неравенство -4 <2x + 6 ≤ 8.

Първо трябва да се изважда винаги 6. получите: -10 <2x ≤ 2. Теперь нужно разделить на 2. Неравенство примет вид: -5