Лекция Tovo работа
2. декартово произведение. Кардиналност.
2.1.Dekartovo продукт на комплекти.
наредена двойка
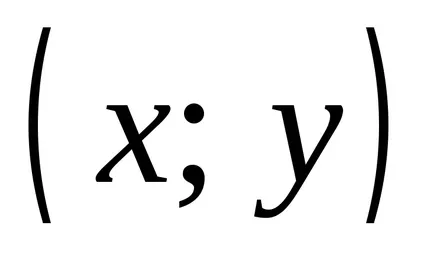
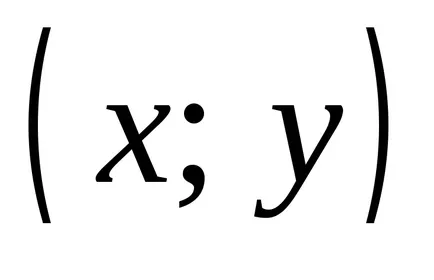
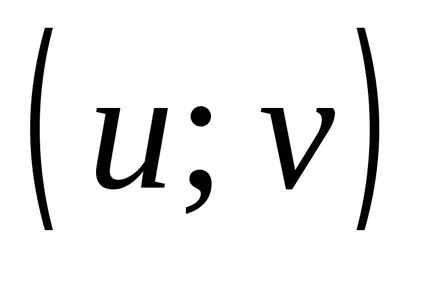
Определение 2.1. Нека А и Б - два комплекта. Директен (декартови) продукт на две групи А и В е множеството от всички подредени двойки, където първият елемент на всяка двойка принадлежи към втория член А. Б:
.
Primer.. нека
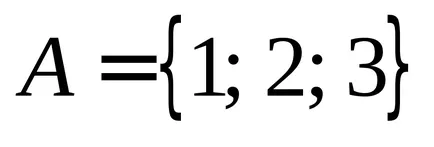
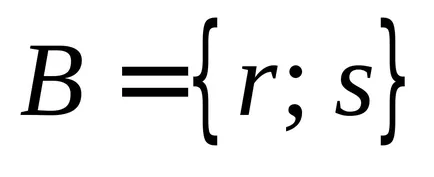
.
.

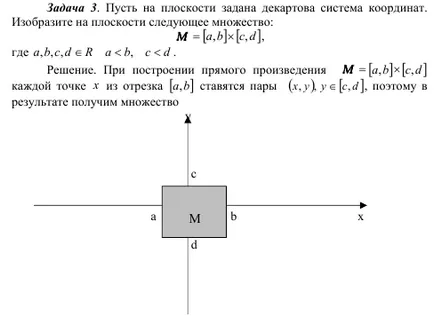
Решение. Първият набор от пуснати на говедото на ос. вторият по оста OY. Наборът от всички двойки, т.е. Декартово произведение, представителният точка на сенчести правоъгълника, но без лява и долната страна.
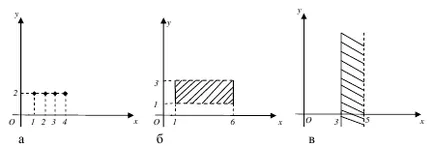
В общия случай, точка на самолета може да бъде определена от подредена двойка координати, т.е. двете точки на координатните оси. Ето защо, на координатната равнина може да се определи като
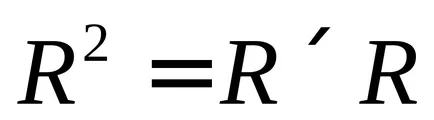
Диаграма на Вен, илюстрираща декартови продукт AxB
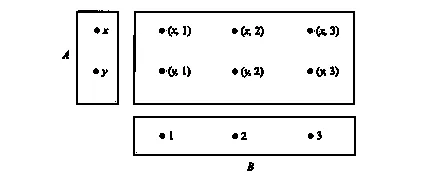
По-специално, ако А или В е празна празна, тогава по дефиниция А B празна.
Концепцията може да се обобщи пряк продукт.
.
Ai комплекта не е задължително да са различни.
Степента на А се нарича директен продукт върху себе си. обозначение:
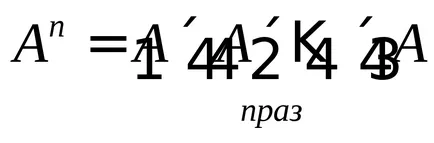
Следователно, като цяло.

Решение. Вп набор се състои от последователности от нули и единици с дължина п. Те се наричат стринг или малко низ с дължина п.


Твърди се, че между набори А и Б имат установява съответствие едно към едно. ако всеки елемент на зададете съответства на един и само един от елементите на В и всеки елемент от набор B съответства на елемент от набор А. В този случай казваме, че поставя и Bizomorfny и използват обозначението A B.
Определение 2.2. Два комплекта А и В са еквивалентни. или equicardinal. Ако между тези комплекти може да се инсталира една кореспонденция. В този случай, моля, напиши: A B. или A = B , и се казва, че комплекта А и В имат еднаква сила.
1) Наборът от десетични числа, еквивалентни на снимачната площадка на пръстите на ръката на човека.
2) Комплектът дори положителни числа (2N), еквивалентни на набор от естествени числа (N).
Определение 2.3. Множество нарича ограничен. ако това е еквивалентно Йоан за някои п. където Jn = 1, 2, ..., п - множество първи п положителни числа.
Определяне А. 2.4.Moschnostyu крайно множество, което съдържа елементи К, е броят на елементите. Тя е посочено A = к. Празното набор се счита за краен брой елементи равно на нула, т.е. = 0.
Така, ако определи разбира се, т.е. A = к. След това елементите на А винаги може да се преномерират. че се поставя в съответствие с номера на елемент от сегмента на естествени числа 1..k от някои процедура. Наличието на такава процедура се разбира, когато се използва запис А = a1, а2, ..., ак .
Комплектите, които не са окончателни, наречени безкрайни. Ако множество еквивалентни на набор от естествени числа N. т.е. А N. тогава зададете е броим. Countable набор А - е набор от всички елементи, които могат да бъдат номерирани в безкраен а1 последователност, а2, ..., с. ..., така че когато всеки елемент е само един номер н и всяко естествено число N ще бъде броят на само един елемент от набор А.
Силата на изброимо множество обикновено се означава с
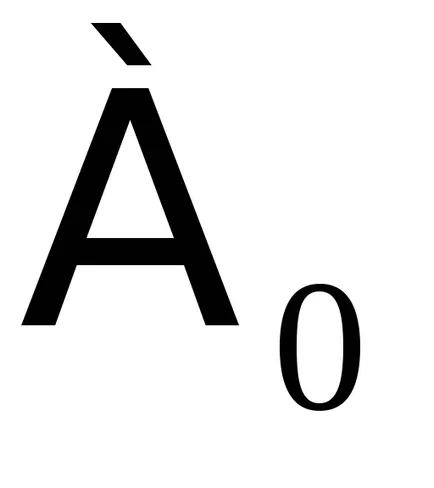

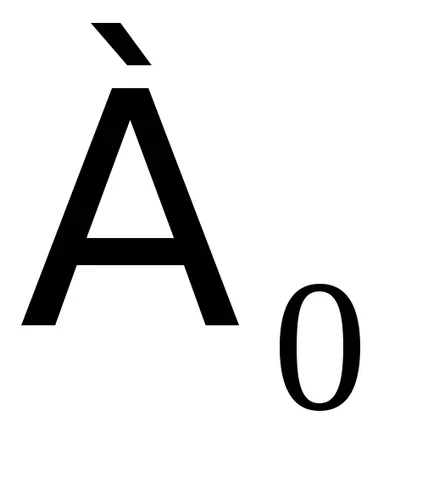
Най-малката безкрайна власт - властта на множеството на естествените числа
Primer.7. Наборът от Z - набор от числа е изброимо.
Решение. Помислете за набора от цели числа Z:
На пръв поглед изглежда, че този комплект не може да се преномерират. Все пак, това номериране може да бъде направено чрез прилагане на следния трик: да не се движат в една и съща посока, и през цялото време, за да го промените.
С други думи, ще се номерират както следва: номер 0 ще даде номер 1, номер 1 - брой 2, номер 1 - брой 3, номер 2 - No. 4, броят 2 - стая 5 и т.н. По този начин, ние получаваме 12:59 кореспонденция между набор Z и N. Това означава, че комплект Z е броим.

Множество наречен несметен. ако силата е по-голяма от силата на набор N. В този случай, на снимачната площадка, се нарича път А или континуум. Силата на континуум е показана
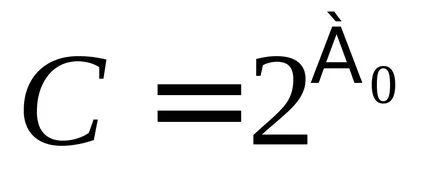
Теорема 2.1. Множеството от всички реални числа има кардиналност на континуум, т.е. R = С
2.3.Teoremy събиране и умножение.
принцип включване-изключване.
Теорема 2.2. (Теоремата на добавяне)
нека
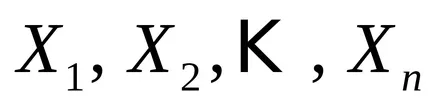
Доказателство. Ние доказваме теоремата чрез индукция.
.
Най-индуктивен стъпка. Да предположим, че теоремата е вярно за п. Ние показваме, че за п 1 също е вярно. след това
Теорема 2.3. (Умножение теорема)
Нека ограничен набор
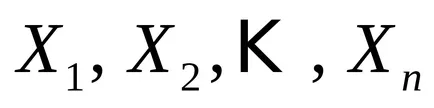
т.е. броя на елементите на декартово произведение на комплекта е равна на произведението от броя на факторите елементи.
Доказателство. Ние доказваме теоремата чрез индукция.
В основата на индукция. Нека п = 2. Нека набор Х1 = А и X2 = Б. мощност, които са съответно К1 и К2. т.е. A = k1. B = k2. Първият компонент на поръчаните двойки може да бъде избран К1 техники, а вторият - начини К2. По този начин, има съвсем различно k1k2 нареди двойки. по този начин,
.
Най-индуктивен стъпка. Теоремата е вярно за п. Ние показваме, че това е вярно, за п 1. В момента има:
Primer.. Колко числа между 0 и 1000, съдържащи точно един номер 6?
Решение. Нека S - набор от числа между 0 и 1000, съдържащи точно една фигура 6. Помислете три подгрупи S1. S2 и S3 на комплекта S.
S1 - комплект, който съдържа номер, който се състои от една цифра и фигура 6;
S2 - комплект, съдържащ двуцифрено число с точно една цифра, равна на 6;
S3 - комплект, съдържащ трицифрено число с точно една цифра равна на 6.
Зададената S1 съдържа само един елемент - броят 6. Следователно, S1 = 1.
Във всеки елемент на комплект S2, съдържащ 6, има или първата или втората цифра. Ако 6 - второто число, тогава има 8 различни числа, които ще се стопи, на първо място, тъй като първото число не може да бъде 0 или 6. Ако 6 - първата цифра, номерата на 9, тъй като втората цифра може да бъде 6. По този начин , S2 съдържа 8 + 9 = 17 елементи, т.е. S2 = 17.
Елементът на S3 съдържа 6 като първата, втората или третата цифра.
Ако 6 - първата цифра, след това има 9 избор на втората цифра и 9 избор на третата цифра. Според комбинаторна принципа на умножение, S3 съдържа 99 = 81 номера с първата цифра 6.
Ако 6 - втората цифра, има 9 избор на третата цифра и 8 възможности за избор на първата цифра като първа цифра не може да бъде нула. Следователно, S3 съдържа 98 = 72 номера чиито 6 - втората цифра.
По същия начин, S3 съдържа 72 номера чиито 6 - трето цифра. Следователно, само S3 съдържа 81 + 72 + 72 = 225 елементи, т.е. S3 = 225.
Тъй като и двете mnozhestvaS1. , S2 и S3 разединена, а след това
.
Ние представляват проблем за изчисляване на броя на елементите в съюза
ограничени набори
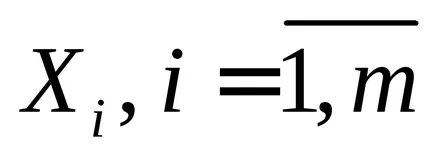
Теорема 2.4. (Принцип включване-изключване).
За крайни множества
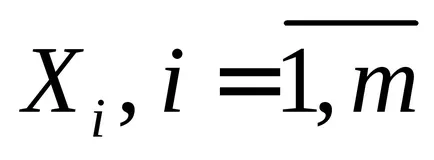
По-специално, за два комплекта, тази формула е под формата:
.
В продължение на три комплекта принцип включване-изключване става:
.
Заглавието на тази теорема подчертава използването на последователни включвания и изключвания на елементи на подгрупи.
Primer.. Колко положителни числа по-малко от 101, са разделени на 2 или 3?
Решение. Нека X - набор от положителни числа, които са кратни на 2 или 3. Помислете две подгрупи X1 и X2 набор от X.
X1 - набор от положителни числа, които са кратни на 2. Броят на елементите или на силата на този набор е равна на
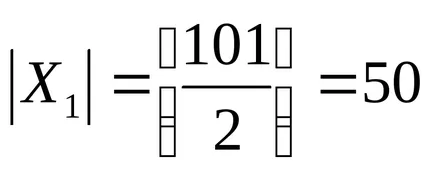
X2 - набор от положителни числа, които са неделими от 3. броя на елементите, или силата на този набор е равна на
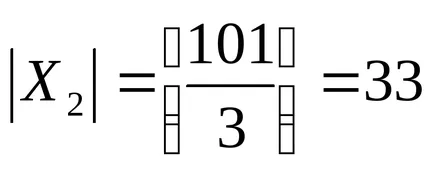
Тогава X1 X2 набор - набор от положителни числа, които са кратни на 2 и 3 и на броя на елементите, или силата на снимачната площадка е равна на
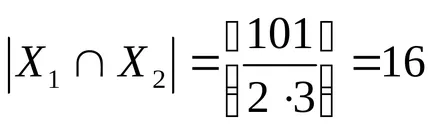
Използвайки формула включване и изключване, за да намерите редица елементи на X.
.