квадратен корен

На корен квадратен от (втора степен корен -) е разтвор.

- икона, наречена радикална.

С други думи, корен квадратен от един - число, което дава за квадратура. Процесът на определяне на стойностите, посочени на корен квадратен от броя на. Най-често Х и включват редица, но и други математически обекти, като например матрици и оператори могат да се подразбират в някои приложения.

Пример за реалните числа като корен квадратен имам обратното, т.е. стойности с различни знаци (в нашия случай, положителни и отрицателни числа), и това усложнява работата на корените. За да се постигне уникалност, въвежда понятието аритметично корен. Неговата стойност в винаги положителен.

Свойствата на квадратен корен.

;

ако ≥ 0 и б> 0;

ако ≥ 0 и п - цяло число;

ако ≥ 0 и п - число.

Забележка (5) 2 = 25, но.

Коренът не може да бъде равен на броя на не-положителен.

- не е възможно да се изчисли корен квадратен от отрицателно число, не съществува.

Ако след това б 2 = а. когато ≥ 0 и б ≥ 0.

Важно е да се разбере, че корен квадратен - е друг входно ниво ½:

фракционна номер степен.

В допълнение, има корен квадратен от корена на куб (трета степен), четвърти и подобни корени. Името на корен се определя от броя на корена.

Забележка: Коренът на всички нива, за да лесно да се представи като частична власт.

Нека да видим как корените са свързани с частична власт. Има х на степен 3/2. Пишем през знака на корена е израз. В знаменателя на дробната мощност кораба до корена, а коренът на числителя на броя.

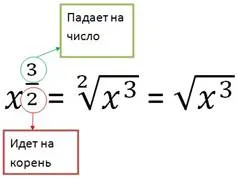
Друг няколко примера:

Само в квадратен корен (коренът на първа степен) не номера на корена. Това е често срещан знак.

Root сила наш степен.

Root сила н степен измежду - е число такова, че за повишаване на степента н -s получи номер.

Коренът на третия, 5-ти, 9-ти - това е, всички корените на странно степен, - се отстранява от положителни и отрицателни числа.

корен квадратен и корените на 4-ти, 10-ти, всички дори сили отстранени само положителни числа.

След това - няколко, така че. Както можете да видите, корените записват като степен с рационален показател.

Не забравяйте, че в основата на една степен по-голяма от нула.

Изразяване равни. В този случай, също, при условие, че е по-голяма от нула.

Примери изчислителни изрази с корените.

;