Критерият на система за линейни уравнения
Критерият на система от линейни уравнения дава Кронекер-Капели.
Леополд Кронекер (1823 - 1891 GG.) # 9472; Немски математик. Теорема, които ще бъдат обсъдени, както се съдържат в неговите лекции в университета в Берлин през 1883 - 1891 години.
Алфред Капел (1858 - 1916) # 9472; Италиански математик. Той, изглежда, даде първото твърдение на теоремата с използването на термина "ранга на" работата си през 1892 година.
За да се гарантира, че системата за линейни уравнения е била последователна, е необходимо и достатъчно условие е рангът на системата е равен на ранга на разширената матрица.
Пример. Проучване на системата за споделена
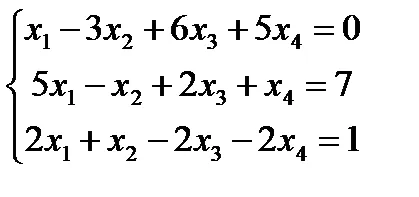
Решение. Събирането матрицата система и увеличен матрицата да ешелон форма ще се извършва едновременно.
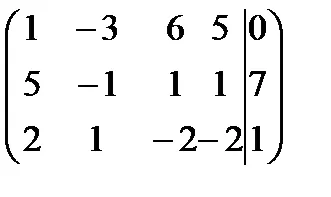
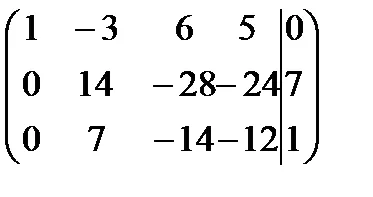
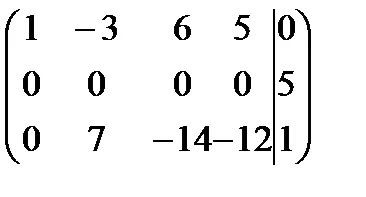
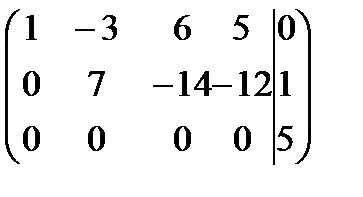
Място система матрици е 2, и ранга на матрицата е удължен система 3. Теорема Кронекер-Капели система е в противоречие.
метод на Гаус за решаване на системи линейни уравнения.
метод на Гаус "се прилага към произволна система линейни уравнения. ние се нуждаем
Определение. Система от линейни уравнения ще се нарича стъпка. ако матрицата на скоростта на системата.
При решаването на система от линейни уравнения, които използваме следния алгоритъм:
1. Запишете увеличен матрицата на системата (1) и да даде да ешалон форма,
определя от ранга на матрицата и разширената матрица на системата.
2. Ако резултатите не са един и същи ранг, тогава системата е в противоречие.
3. Място матрица система е подсилена ранг матрица и е равен на броя R. Най-
този случай, системата е съвместима и трябва да намери своето решение.
4. С помощта на стъпаловидна разширена матрица на системата, се записват най-подходящата система ниво.
5. Ако номер R е равен на броя на неизвестни N, скоростта на системата е на формата
От системата (2) последователно намерите стойностите за x1. x2, ..., х. като се започне от последната уравнението. В този случай, системата (1) има уникален разтвор.
6. Ако броят R-малък от броя на неизвестни, скоростта на системата е на формата
Системата (3) R уравнения и п неизвестни. Неизвестна x1, ..., HJ1 който за първи път се намери в системата уравнения (3), нека да се обади на главния непознатото. друг # 9472; безплатно неизвестен. От (3) последователно се разшири през главния неизвестен наличността от последното уравнение. Безплатни неизвестни могат да вземат всички стойност. В този случай, системата има безкрайно много решения.
2)
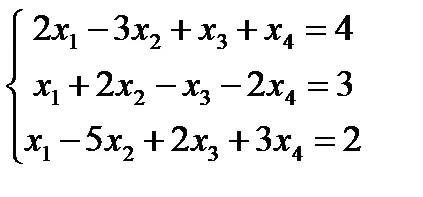
3)
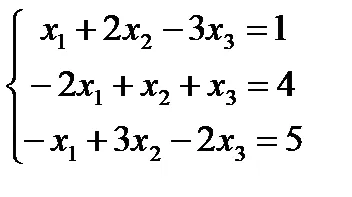
правило Крамър за решаване на системи линейни уравнения.
Gabriel Cramer (1704 - 1752) # 9472; Швейцарската математик, който през 1750 г. бе открита метод за решаване на системи линейни уравнения, по-късно наречен правило Креймър.
Определение. Системата на линейни уравнения се нарича Креймър, ако тялото на уравнения равен на броя на неизвестни и определящ фактор за матрична система е различна от нула.
Теорема 7.1. Cramer система има уникален разтвор, който е в съответствие с формули
където # 9472; детерминанта на матрицата на системата, # 9472; детерминанта, получен от. подмяна на коефициентите на колоната, с колона на свободни условия.
Доказателство. Като се има предвид система Крамър
# 9474; # 9474 А = # 8710; =

Според теорема 3, глава 6 матрична система има обратна матрица А -1.
Пишем системата Креймър (4) във формата за матрица
Увеличаването двете страни на уравнението на матрица (5) наляво от А 1:
Поради асоциативност на умножение на матрици, ние имаме
А -1 (AX) = (А -1 A) X = X = H ET
X = A -1 V # 9472; решение на системата.
1) Нека покажем, че решението е уникален. Да предположим, че X1 и X2 # 9472; Две решения на уравнението на матрица (5). След AH1 = Б и В = AX2 където AH1 = AX2. Произведението на двете Чисти равен на А -1 в ляво, ние имаме
Следователно, системата (4) има уникален разтвор.
2) Намираме разтвор на (4). От уравнение X = A -1 V са:
=
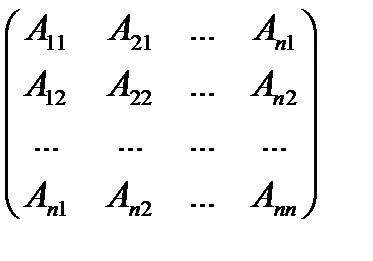
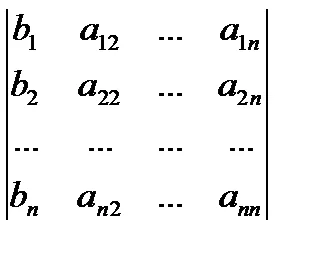
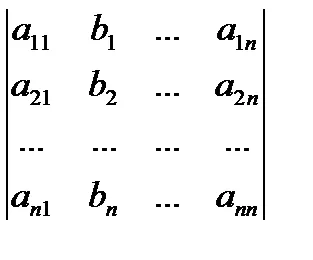
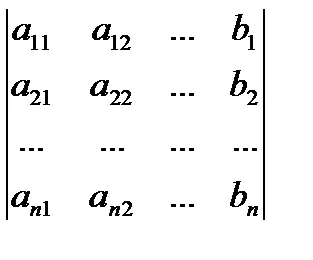
Сочещ детерминанта от дясната страна, съответно, ние получаваме формула.
Пример. Решаване на система от уравнения с правило Крамър