Координира самолети и графични функции

Системата за правоъгълна координатна е двойка перпендикулярни координират линии наречени координатни оси, които са разположени така, че се пресичат в тяхното начало.

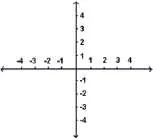
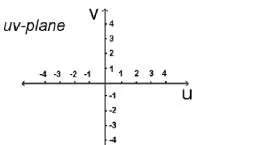
Предназначение писма от координатните оси х и у е общоприето, но могат да бъдат всякакви знаци. Ако използвате буквите х и у, самолетът се нарича ху-равнина. В различни приложения могат да се използват различни от букви х и у писма, и както е показано с чертежи надолу, има UV-самолет и TS-равнина.

наредена двойка

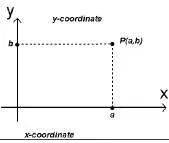
Под наредена двойка реални числа имаме предвид две реални числа в определен ред. Всяка точка Р в координатната равнина може да бъде свързана с уникален подредени двойка реални числа чрез две линии през точката Р: една перпендикулярна на оста X, и още - перпендикулярна на оста у.

Например, ако вземем (А, В) = (4,3), след това на референтните лентите

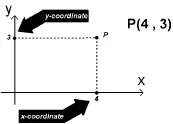
Построяване на точка P (а, б) означава да се определи точката с координати (а, б) на координатната равнина. Например, различни гледни точки са построени в изображението по-долу.

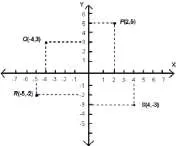
В декартова координатна система оси разделят равнината на четири области, наречени квадранти. Те са номерирани обратно на часовниковата стрелка римски цифри, както е показано на фигура

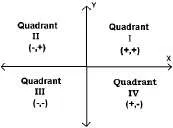
Определяне на график

Графика уравнение в две променливи х и у, е набор от точки на XY равнина, координатите на които са членове на набор от решения на това уравнение

Пример: за изготвяне на графика Y = х 2

Поради факта, че 1 / х е неопределен, когато х = 0, може да се изгради само точки, за които х ≠ 0

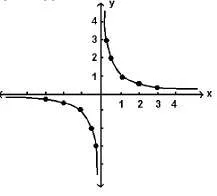
Пример: Виж всички пресечните точки с осите
(А) 3x + 2у = 6
(B) X = Y 2 -2y
(С) у = 1 / х

Нека у = 0, тогава 3x = 6 или х = 2

Това е желаната точка на пресичане на оста х.

След като се установи, че х = 0, ние откриваме, че точката на пресичане ос е в точка у = 3.

Така че EV начин можете да решите уравнението (б) и разтвор (С) е даден по-долу

1 / х = 0 => X не може да се определи, тогава няма пресичане с оста у

у = 1/0 => Y и неопределени => не пресичане с оста у

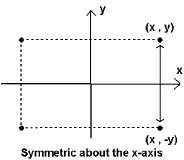
На фигурата под точка (х, у), (-x, у), (х,-ил) и (X, У) означават ъглите на правоъгълника.

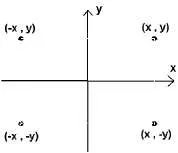
• графика е симетрична около оста X, ако всяка точка (х, у) графика, точка (х,-ил) също е в точката на графика.

• графика е симетрична по отношение на ордината, ако за всяка точка от графиката (х, у) точка (-x, у) също принадлежи към графиката.

• графика е симетрично спрямо центъра на координати, ако всяка точка (х, у) графика, точка (-x,-ил) също принадлежи към тази схема.

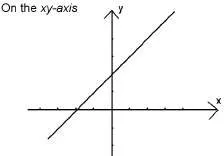
Функция графика на координатна равнина се определя като графиката на уравнението у = е (х)

Графика е (х) = х + 2

Пример 2. Графика е (х) = | х |