Концепцията на логаритъм и антилогаритъма
Има неясноти при използване на експоненциални числа за отбелязване. Ако ние се занимаваме с числа с много нули, това е достатъчно проста. Но да предположим, че е необходимо да се размножават 6837 и 1822. Ако пишем тези номера в експоненциална форма. получаваме: 6,837h10 3 и 1,822h10 3. Умножете експоненциална част е лесно, но какво да се прави с цифрите 6.837 и 1.822? Ние сме изправени пред същата задача като за умножаване на големи числа, като единствената разлика е, че е необходимо да се следи положението на десетичната запетая. С други думи, ние трябва да представлява броят във форма, която не е част експоненциално е възможно най-кратък или равен на 1. Тъй като това е десетична система, ние се нуждаем от десетични експонат.
Сега нека да погледнем по-отблизо на експонентата на базата на 10. Нека започнем с 10 0 = 1 и 10 1 = 10. И това, което са експонентата между 0 и 1? Например, 10 = 0.5 10 февруари = LLO. което е приблизително равно на 3,162278. По същия начин (но с голяма трудност) може да се настрои на 10 степен по между 0 и 1. Тези стойности са изчислени и се събират в специални директории във вид на таблици.
Тъй като в този случай е винаги няколко основа 10, таблиците обикновено са само експонати. че е експоненциално. Отделно записани на изложителя се нарича логаритъм, експоненциалното стойността на израз под формата на обичайния брой се нарича антилогаритъма. Например, в експресионен 10 февруари = 100 имаме следните наименования: -
и 100-2 Антилогаритъмът.
Таблицата по-долу, която показва броя на логаритми да antilogarithms наречени маса antilogarithms.
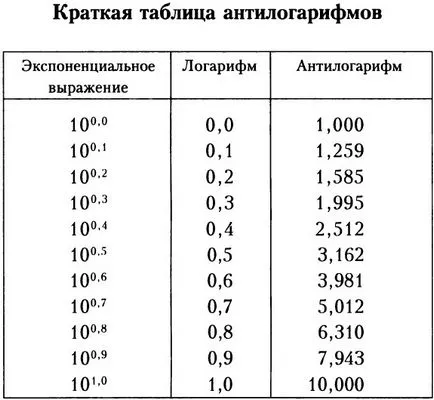
Таблицата показва приблизителни стойности antilogarithms и е невъзможно да се даде точни стойности, защото те съществуват само за такива числа като 10, 00 10 10 и така нататък. Въпреки антилогаритъма стойност може да бъде изчислена с точност (т.е., до такава знак), което се изисква в конкретния случай.
Ако тръгнем в обратната посока, можем да всяко число от 1 до 10 представени като 10 в известна степен. С други думи, за всеки номер, като се използват подходящи техники може да бъде изчислен еквивалент логаритъм.
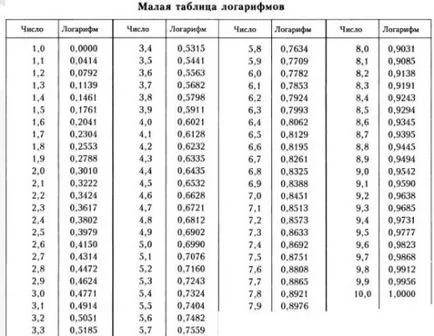
По-долу е обобщена таблица на логаритмите за брой обикновени числа. Подробни таблици с логаритми, където можете да намерите на дневника за всяко число, съдържащо се в редица директории.
Допълнително съдържание:
Сподели с приятели: