Йеленя оптимална големина много

Резерви свирят както положителни и отрицателни роля в системата за логистика. Положителна роля е, че те осигуряват непрекъснатост на производствения процес и на продажбите, като един вид буфер, изглаждане непредвидени колебания в търсенето, нарушаване на сроковете за доставка на ресурси, подобряване на надеждността на управлението на логистиката.

Недостатъкът на създаване на резерви е, че те са имобилизирани значителни финансови средства, които сега могат да бъдат използвани за други цели, например, инвестиции в нови технологии, проучване на пазара, подобряване на икономическите резултати на предприятието. В допълнение, по-големи нива на запасите от готова продукция възпрепятстват подобряването на нейното качество, тъй като компанията е преди всичко се интересуват от прилагането на съществуващите продукти, преди да инвестират в подобряване на нейното качество. Въз основа на това, там е проблемът за осигуряване на непрекъснатост на логистиката и процеси, най-ниското ниво на разходи, свързани с възникването и управлението на различни видове запаси в логистична система.

Един от методите за ефективно управление на инвентара - определяне на оптималните за превози на доставките, което оптимизира разходите за транспортиране, съхранение на стоки, както и за да се избегне излишната или недостиг на стоки в склада.

Оптимален размер на партидата qopredelyaetsya на критерия за минимални разходи за транспорт и съхранение на инвентара на продукта.

Големината на общите разходи се изчислява съгласно формулата (3.1);

Къде - транспортните разходи за текущия период (година), щатски долари;

- разходите за съхранение на резерви за периода на сетълмент (година), USD

Стойността определя по формулата:

Къде n- броят на партидите, доставени през периода на плащане,

- тарифата за превоз на една от страните. USD / партия.

Разходите за съхранение се определя от формула (3.4):

= *

Къде QSR - среден размер (в тонове), който се определя на предположението, че новата партия е доставена след като предишният е напълно изтощена. В този случай средната стойност, изчислена по следната формула:

Заместването експресия върби формула (3.1), ние получаваме:

С обща функция на разходите има минимум на мястото, където първото производно по отношение qravna нула, т.е.

Решаването на уравнение (3.7) по отношение на оптималния размер qpoluchim график линии:

Тъй като размерът на годишните обем Приети данни за потреблението производствени получени от прости средно метод за прогнозиране: Q = 98 т / г ;. тарифата за транспортиране на една партида = 80 USD / тон; разходите, свързани с съхраняване на запаси = 5 $ / тон.

Замествайки тези стойности, получаваме:

В този случай, общите разходи са както следва:

Решението на този проблем е графично нанасяне (р), (р) и С (р), след извършване на необходимите изчисления за определяне и С

Ние дефинираме стойностите С и при izmeneniiqv диапазон от 400 до 800 със стъпка 100. Резултатите от изчисление, са изброени в Таблица 3.1.

Според Таблица 3.1 нанесени разходи (транспорт, съхранение и обобщените) на размера на партидата (Фигура 3.1).

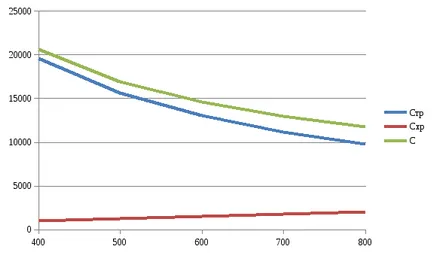
Анализ фиг.3.1 графики показват, че

Изчисляването на оптимален размер на много от дефицит на стойността на разходите, свързани с дефицит = 15 $ / тон.

В контекста на недостига стойност Q *, изчислена с формула (3.8) се довежда до koeffitsientk, като се вземат предвид разходите, свързани с дефицит.

Коефициент krasschityvayut формула (3.10):

- стойността на разходите, свързани с дефицит;

Заместването на ценностите, получаваме:

р = 1,15 * 1770,9 = 2036,5 (т)

От това следва, че при условията на възможен недостиг доставка оптимален размер на партидата да се увеличи с 15%.