Изчисляване крива дължина дъга л, дефинирани в полярен координатна система
Нека крива L е дефинирано в полярни координати:
= =
= =
=

Дължината на дъгата на кривата в полярна координатна система L =.
Пример: Изчислява дължината на кардиоидна. Чрез симетрия изчисляваме кривата ½ дължини. ½L = = =
= = = = =
= =
½L = =
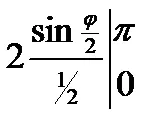
Да предположим, че във формулата за L = долната граница на дължината на дъгата остава постоянна, а горната граница се променя. За да се подчертае това, горната граница е обозначен с буквите х. и променливата на интеграция - буквата б. Като се има предвид, че дължината на дъгата L е функция на горната граница, получаваме:

Според теоремата на производната на интеграл горната граница на тази функция е диференцируема и неговите производни се изчислява по формулата:
Следователно дъгата диференциални дл или в съкратен, DL = DX. Тъй като. след дл =
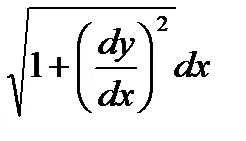
Като се има предвид този резултат и на факта, че разлика от функцията, равна на тангента на нарастване ордината води до следната геометрична диференциал смисъл дъгата: дл диференциал дължината на дъгата сегмент е допирателната от точката на докосване с абсциса х до точката с абсциса х + DX.
Въпроси за самоконтрол:
1.Zapishite формула за изчисляване на дължината на дъгата на кривата, дадена в декартова координатна система.
2.Zapishite формула за изчисляване на дължината на дъгата е определено по параметри.
3.Zapishite формула за изчисляване на дължината на дъгата, определена от полярна координатна система.
4. Как геометричен смисъл на разликата в дъга?
Задачи за независим решение:
1.Nayti дължина на дъгата от парабола на х = у = 0 = 1 DOX.
2. Да се намери дължината на дъгата на кривата X = на. у = от т = 0 до т = 1.
3.Nayti кардиоидна дължина дъга г = 2.
Решаването на типични задачи:
Пример 1: намери дължината на линия от точка
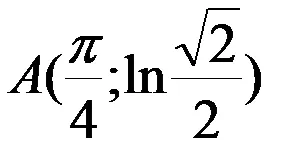
Решение: Линията е посочено в Декартова координатна система. Очевидно е, че

Тъй като се счита интервала. на

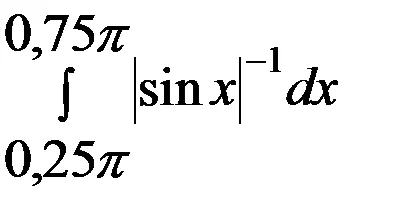
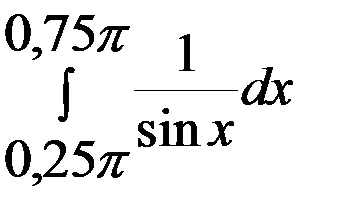
=



Имайте предвид, че при изчисляването на интеграла ние използвахме замяната:
Пример 2. намери дължината на кривата
.
Решение: кривата се определя по параметри. Лесно е да се види, че
= =
= =
= =


Тъй като интервалът равноправието
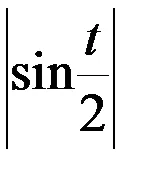
=

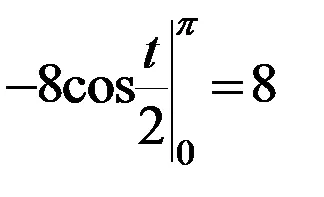
Намери дължината на дъгата на кардиоидна R = себе си (1 + COS
Решение: кардиоидния е симетрична около полярната ос. Чрез промяна на полярен ъгъл от 0 до. получаваме половината от дължината на Кардиоидните:
Цялата дължина на кардиоидна L = 2
Може да се покаже, че даден от уравнения х = х (Т) на дължината на дъгата на кривата на място, у = Y (т), Z = Z (т). , Той има следната формула: