Изчисление на случайни грешки
2. технически грешки в изчисленията
3. Изчисляване на брутните гафове и грешки
4. Изчисляване на случайната грешка означава, Excel
Не измервания може да не са напълно точни, обаче, за всяко измерване, измерената стойност на количеството е винаги различна от истинската му стойност.
Целта на експериментатора е не само намирането на самата стойност, но оценката, направена, когато измерената грешка. В зависимост от свойствата и причините разграничи систематични и случайни грешки и гафове.
Наречен систематична грешка, която, когато се повтори измервания, извършени от един и същ метод се използва същата апаратура, остават постоянни.
Систематичните грешки, причинени от фактори, които действат по същия начин, когато множество повторения на същите размери. Те съответстват на отклоненията на измерените стойности на истината е винаги в една и съща посока.
Систематичните грешки могат да се дължат, от една страна, повреда или неизправност в употреба устройства (например, неправилна инсталация на "нула"). На второ място, те могат да бъдат причина за несъвършенството на техниката за измерване, използвани или пренебрегване на постоянни фактори, влияещи върху явлението се разследва. Например, възможно е да се получат по-високи стойности на температурата на топене кристал, ако измерванията се извършват при повишено налягане на външен.
Отделно от грешки, възникнали по време на измерванията, системни грешки са свързани с използването на формули за приближение и грешки поради разликата на реалния обект на приетия модел.
грешка инструмент е разликата между показанията на всяко устройство и истинската стойност на измерваната величина. Тя може да съдържа произволни и систематични компоненти.
Фишове (или груби грешки) се появяват обикновено води до рязко отклонение от останалите индивидуални измервания. Подхлъзвания се дължат главно на липса на внимание експериментатор или неизправност на измервателни уреди. Резултатите от тези измервания се изхвърлят.
Наречен случайни грешки, които при многократни измервания при същите условия се променят по непредсказуем начин.
Случайни грешки са причинени от неконтролирано множество причини, ефектът от което не е едно и също във всеки експеримент. В резултат на измерването на същата стойност няколко пъти при същите условия се получава серия от стойности на това количество, които се различават от истинската стойност на случаен принцип.
Изчисление на случайни грешки
Природа случайни грешки могат да варират колебания нулево положение измерване указател инструмент; несъвършенство на сетивата на опита (например, невъзможността да започне хронометъра в точния момент); случаен неконтролирана промяна на външни влияния - температура, влажност, налягане; прослушване в електрическата верига, и т.н. което е почти невъзможно да се вземе предвид.
Да предположим, че количеството X се измерва N пъти:
Обработката на задача на експерименталните данни от измервания е да се определят границите на интервала, в който се намира истинската стойност на измерваната величина.
Като следната форма на резултатите от измерванията на всяко количество:
За най-вероятната стойност на X средната аритметична стойност на резултатите от измерванията:
Най-голям е броят на измерванията, колкото по-близо до истинската средна стойност.
В присъствието на случайни грешки при измерването, абсолютната грешка на метод на студента се определя, както следва
при което - стандартно отклонение, - фактор Student - надеждност, количество, равно на вероятността, с която доверителен интервал включва X. истинската стойност
Например означаваме точки върху резултатите на редица линия. Те са струпани около средната стойност.
Скоби означават доверителен интервал, в който R5 са експериментални стойности на 10, т.е. доверие veroyatnostP 0.5. Квадратни скоби съответства на доверителен интервал за 0,8 вероятността P.
В лабораторни физическа практическа стойност от приет безопасност.
KoeffitsientStyudenta и корекция се използва за коригиране на доверителния интервал, с малък брой измервания (N<30).
KoeffitsientStyudenta може да бъде изчислено в рамките на теорията на вероятностите.
Водени метод raschetapri малък (п = 3¸10) брой на измерванията винаги са прогнози.
Ако оставим на броя на измерванията до безкрайност, и з интервал # 61485; до нула, хистограмата става непрекъсната граница крива, която е крива на разпределение на грешка. При определени условия, които обикновено се извършват по време на измерването, тази крива представлява Gaussian функция със следната форма:
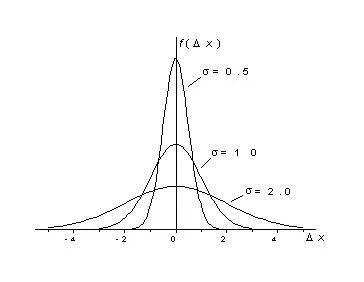
където параметъра # 61555; определя широчината на разпределението. Няколко Gaussian криви за различни стойности на параметъра # 963; показано на фигура 2.