Графично решение на линейното програмиране проблем

Както е известно, на широката Задачата на линейното програмиране се състои в намирането на стойностите на променливите, които отговарят на определени линейни ограничения и осигуряват най-високо (най-ниската) стойността на конкретно линейна функция. Например, изискването:

В ролята на неизвестни количества може да бъде, например, обема на производството (на обувки, уреди за нощно виждане и микроскопи), разпределението в брой при ликвидация на порутени жилища и изграждане на здравни заведения, с тираж от стихотворения М. Ю. Lermontova и "заговор против уроки."; ограничения, свързани с консумацията на материали, наличието на предимства за някои видове публикации, пазарни условия или лични предпочитания, както и обективна функция L на (X) може да се определи печалбата от стоки, произведени или размера на неусвоените средства.

Може да откриете, че проблемът е нерешим - няма план (ограничения в противоречие помежду си). Може би единственият план, или много (много) планове, сред които е необходимо да се намери най-добрата (оптимално), което съответства на максималната печалба (морално удовлетворение, степен на пречистване на вода) или минимална цена (оплаквания на граждани, а на дървесни отпадъци и т.н.).

Измерението на действителните задачи обикновено са високи (от десетки до няколко стотици). Тук ние ще чрез примера на двуизмерни проблеми да даде на читателя ясно, графично представяне да бъде решен чрез линейни програми (приема се, че всеки човек е в състояние да привлече върху плоска лист хартия и да се изграждането на триизмерното пространство около нас). Наличието на такова представителство може също да помогне в обобщаващи заключения bulshey мащабни проблеми.

Естествено, за решаване на проблема, е желателно първо да получите представа за разнообразието на планове (приемливи решения), и едва след това от снимачната площадка, за да изберете най-доброто (от гледна точка на целта).

Тъй като системата ограничава двумерен линейното програмиране определя точките на настройка на самолета, лежащи или правите линии, или половин равнини, оградени от тези линии, множеството от планове могат да бъдат представени с по една точка, част от права линия, като тази цифра, наподобяващ изпъкнал многоъгълник, но не елипса, полумесец или друго изпъкнало обект.

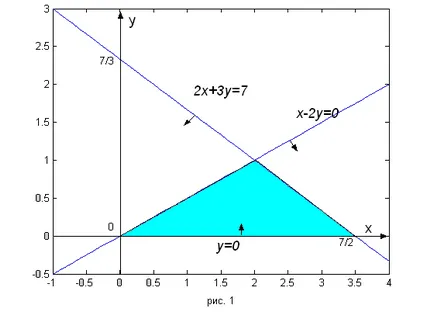
Така че, ако проблемът се свежда до описание на условията на 2x + 3y ≤7. Y ≥0. х- 2y ≥0. оригиналната конструктът съответните прави линии (права 2х + 3Y> = 7 с координатните оси на точките на пресичане, права линия у = 0 съвпада с 0x на ос; насочва х- 2у = 0 преминава през началото и е, например, точка с координатите х = 2. Y = 1). По този начин "комплекс" от сграда, да разберете това, което е приемливо за съответното неравенство, което е достатъчно, за да го носите навсякъде, в равнината не лежи на права линия, и се уверете, ограничения вид половин самолет. Например, за да се провери първа граница (съответстваща на линия не премине през произход) може да точка (х = 0. Y = 0), за да се гарантира, че 2 · 0 · 0 + 3 <7. Следовательно, эта точка со всеми ее «соседями» до прямой линии (полуплоскость, её содержащая) соответствует неравенству 2x+ 3y ≤7. На рис. 1 приемлемые полуплоскости выделены стрелками и общая их часть (множество точек, удовлетворяющих всем трем условиям; множество планов) представлена выделенным здесь треугольником.

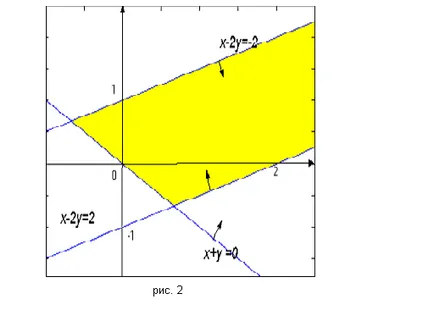
Построяване на съответния три прави и намирането на подходящ полуравнина, ние откриваме, че много планове - неограничен полигон (триъгълник, един връх, от които ", изпратени до безкрайност"), показана на фиг. 2.

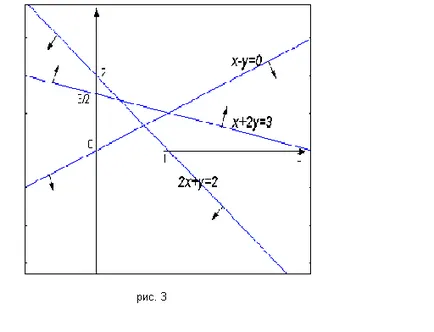
Ако сте приели системата на ограничения на формата х + 2у ≥3. 2x + у ≤ 2. X-Y ≥ 0. че е лесно да се види (Фигура 3.), че нито една точка, която ще задоволи всичките три условия, не можете да намерите - противоречиви ограничения (за устройство на празен).

Какви изводи могат да се направят от тези примери?

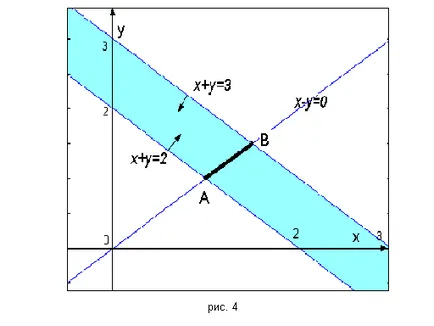
Множество двуизмерни планове на линейното програмиране проблем е изпъкнал многоъгълник (ограничена или неограничена), сегмент права линия (ограничена или неограничена) точка или отсъства поради противоречиви ограничения (няма извити или не-изпъкнали форми).

Сега, като си спомни нашата цел, нека се запитаме: какви намери набор от планове е оптималната (осигурява най-голяма (поне) стойността на нашата целева функция)?

Равен схематично не само множество планове в равнина (х, у), но целевата функция Z = L (х, у), триизмерното пространство изобразен равнина, където Z стойност представлява отстраняване на тази равнина от равнината (х, у). Очевидно е, че най-голямото и най-малкото разстояние от множеството планове е случаят в някои от своите върхове, но не и в своите вътрешни точки (фиг. 5).

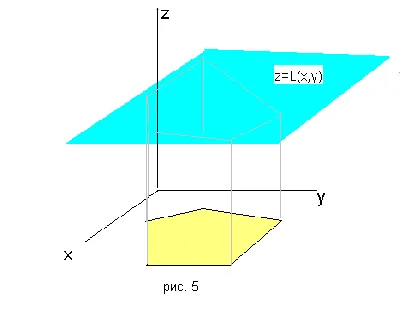
Ако този образ не ви осигури в този (или забравя, че уравнението на равнината, в триизмерното пространство може да бъде представена чрез линейно уравнение на α · х + β · у + γ · Z = С), привличане концепция помощта на градиент функция - вектор, състоящ се от: негови частични производни, които показват по посока на най-голямото нарастване на функцията в близост до точката. За нелинейни функции на наклона варира от точка до точка. Например, ако е (х, у) = х2 + XY. на gradf (х) = 2x + Y, X> в различни точки променя своята ориентация. В случай на линейна функция, която представлява градиент съвпада с неговите коефициенти, например Градл (х, у) = 2х + 5Y> = 2, 5> и градиента остават непроменени във всички точки (по-специално във всички точки на набор от планове).

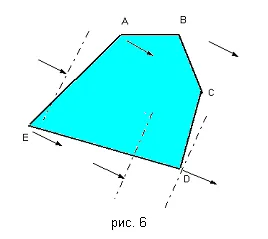
Фиг. 6 ние показахме много планове за изпълнение на задачи (ABCDE полигон) и се вижда от посоката на стрелката на градиента. Изборът всички вътрешни точка на снимачната площадка на планове, ние виждаме, че в близост до него може да се намери друга точка (отместването в градиента или обратно) в bulshim (малка) стойност L (X, Y). Очевидно е, че в този случай максималната се достига при точка D. и минимална точка -да Е. Разбира се, ако наклонът е перпендикулярна на лицето на набор (линия сегмент), на екстремум се постига при всички точки на сегмента (по-специално, в краищата).

Това предполага, че при търсене на екстремум точки (максимална и минимална) на линейната функция (оптималните планове), е достатъчно, за да се разгледа само най-горния набор от планове. но не и своите вътрешни точки. Освен това, в двумерния случай на достатъчно точни, за да мащабирате конструкции не може да мине през всички върхове (броят разбира се, но може да бъде сравнително голям) и веднага се вижда до крайност.

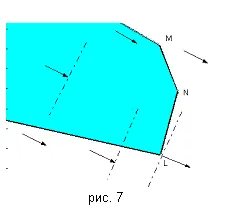
Имайте предвид, на фиг. 7. където много планове е неограничен. Чрез изграждане на наклона на целевата функция, то е лесно да се види, че максимумът се достига при който ъгълът на Л. като има предвид минималната функция не е ограничено (поне L (X, Y) → -∞). Този пример показва, че в случая на безкраен набор от планове може да покаже neogranichennostL (х, у) на максимум, минимум, или и на двата критерия.

По този начин, графично решаване на двуизмерни линейни програми може да доведе до следните резултати:

• намерено оптимално план (може би повече от един);
• разкри липсата на оптималния план (задачи противоречиви ограничения или целева функция не се ограничава поради безграничната набор от планове).

Ако все още имате някакви съмнения, обърнете се към следните примери (тук ние вместо получени в училище математически символи х и у използването символи x1 и x2, надявам се, че тази промяна няма да ви води към объркване).

Пример 1. Ние се реши проблема с максимизиране

Решение. Намери набор от изпълними решения (планове) проблем, т.е. множеството от точки (x1, x2), което отговаря на определени системни ограничения (1) - (5), които са изграждане на половин самолет, съответстващ на ограниченията на проблема и да се определи тяхната обща площ.

Ние приемаме първата от условията и изграждане на права линия -Х1 + 2x2 = 6. За тази цел ние откриваме всеки две точки, като пресечната точка с координатните оси: ако x1 = 0x2 = 3 и Х2 = 0x1 = -6. т.е. точката (0, 3) и (-6, 0). За да се изолира съответната половина равнина по отношение на изградените линия заместващи координатите на всяка друга точка (например, произход) от лявата страна на неравенството (1). По този начин, когато се замести стойностите на x1 = 0 и Х2 = 0 виждаме, че състоянието е изпълнено (0 ≤ 6). Следователно, границите на допустимите разтвори на това неравенство -Х1 + 2x2≤6 - че полуравнина, която включва произхода. Показване на втория ограничение е абсолютно идентични.

Що се отнася до трети ограничения половин самолет, той се намира във връзка с граничната линия от другата страна, а не на произхода.

Четвъртият и петият граница (x1≥0. X2≥0) съответства на половин равнини, които се намират от дясно на ординатата, а по абсцисата (първи квадрант на самолета).

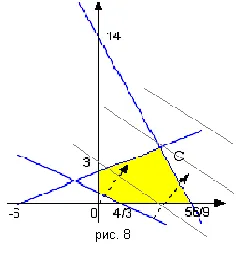
В резултат на това, ние получаваме общо пространство за всичките пет половин самолети (много планове) - изпъкнал петоъгълник (Фигура 8.).

Сега ние използваме градиента на функция L (х) = 2x1 + 3x2. Има Градл (х) = (2. 3). Този вектор конструкт на фигурата в броенето от произхода (или от всяка точка на равнината или от всяка точка на планове). Ако точката за екстремални не е очевидно, вземете "нишка", която е перпендикулярна на наклона и плъзнете върху тези от тях планове в посока на функцията за наклон.

Имайте предвид, че във всички точки на "конци" стойност на целевата функция по същия начин (като "ниво линия", което виждате, например, по отношение на физическия карта на света с образа на планини и дълбочина).

Лесно е да се види, че последната точка на контакт "нишки", с много планове е необходима максимална точка на функция L (х) (първа точка на контакт - минималната точка). В нашия пример, максималният точка на функция L (х) е точка В. Остава да намери своите координати.

Тъй като е получена от пресичането на първата и втората прави линии, е достатъчно за решаване на система от две уравнения с две неизвестни

Лице, запознати с определящите фактори и управление на Креймър, реши във формата:

Ако читателят не счита, цената на труда, той може да бъде решен чрез заместители, или всяка друга техника.

Пример 2. Виж екстремните стойности на функцията