Гости - GDZ математика, алгебра, геометрия, клас 2-11
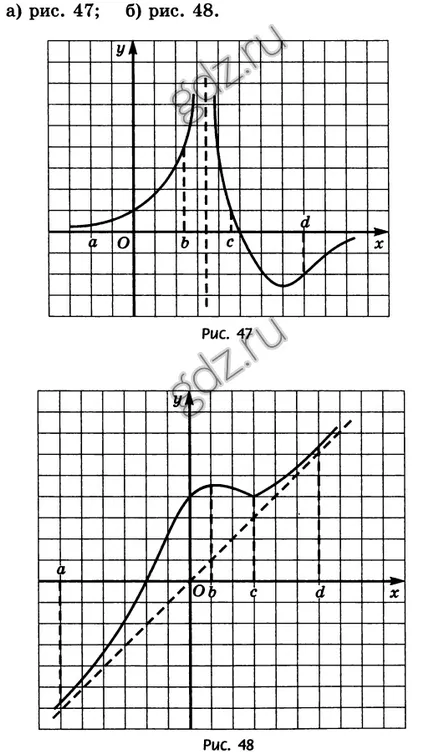
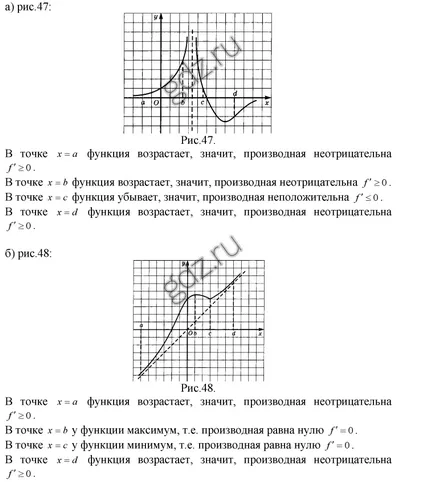
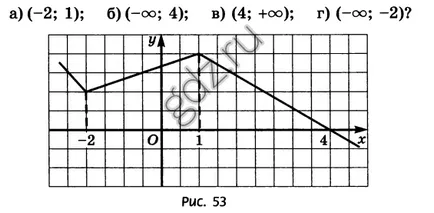
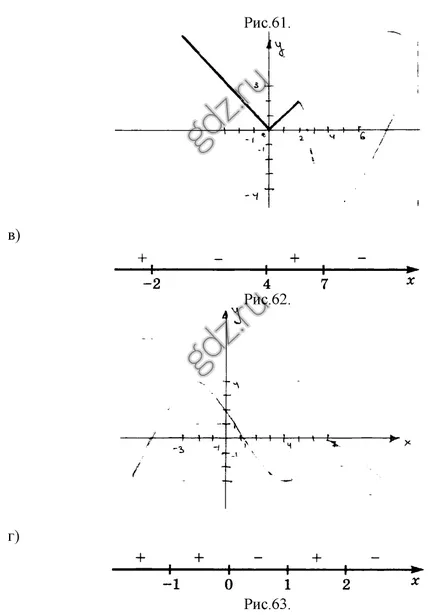
30.1 Определяне който знак е производно на у = е (х) в точки с абсциса, а, б, в, г, ако функцията график е показано на чертежите:
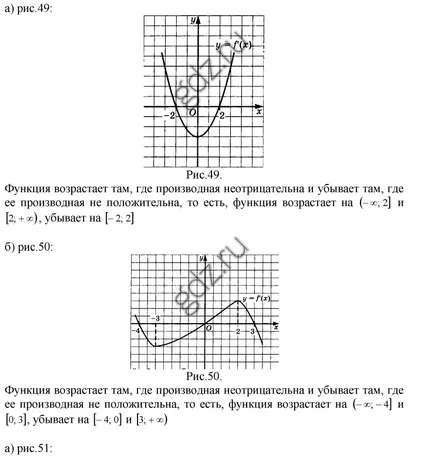
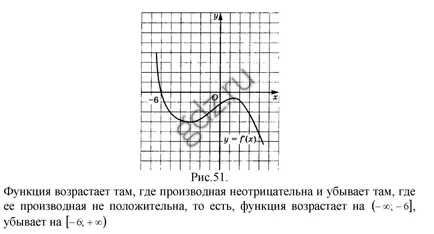
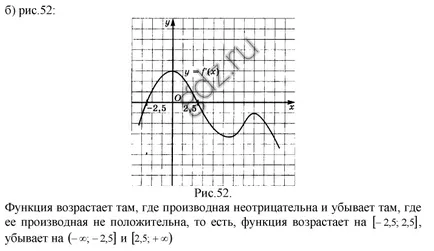
30.2 Определяне на интервалите на увеличаване и намаляване на функцията чиято графика е показано по-долу:
30.3 график производно е показано на фигурите, определят пропуски функция у = F (х) се увеличава, и в които: - намаляване:
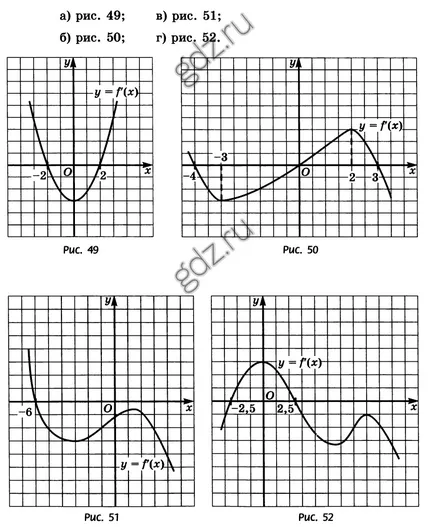
30.4 В някои от тези пропуски функционира у = е (х) намалява, ако графиката на негово производно е показано на Фигура 50:

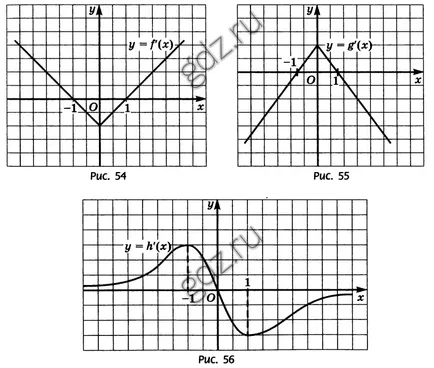
30.5 определи кои от функциите за у = е (х), у = грам (х), Y = H (х) интервала [1; 1] е период на увеличаване, ако на Фигури 54-56 са графики, производни на тези функции:
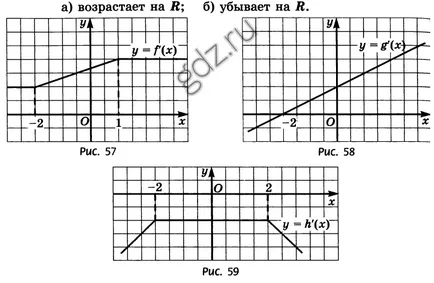
30,6 Фигури 57-59 са графики, получени функции у = е (х), у = грам (х), Y = H (х). Определя които функция у = е (х), у = грам (х), Y = H (X):
30.7 направи скица графика на производно функция у = F (х), ако е известно, че функция у = F (х) се увеличава по протежение на линията (-∞ 1] и намалява по линията [1 + ∞).
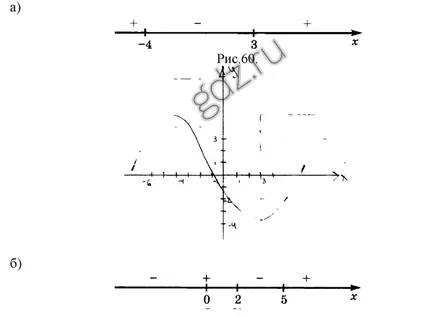
30.8 направи скица графика на функция у = е (х), ако знака на деривати постоянни интервали F '(х), показана по предварително определен образец:

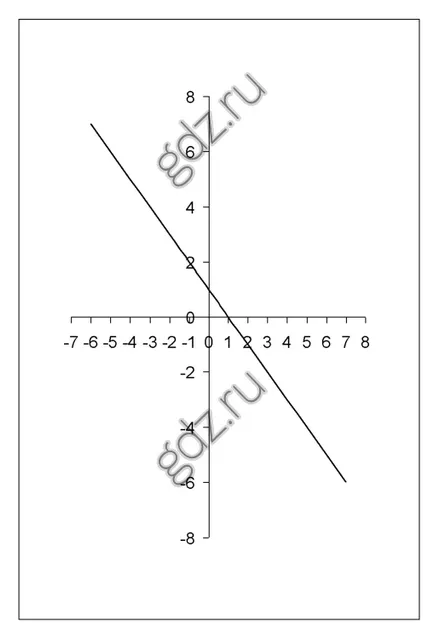
30.9 Покажете, че дадена функция се увеличава:

30.10 Покажете, че дадена функция се намалява:
30.11 Докажете, че функцията е монотонно върху цялата реална линия; посочете естеството на еднообразието:

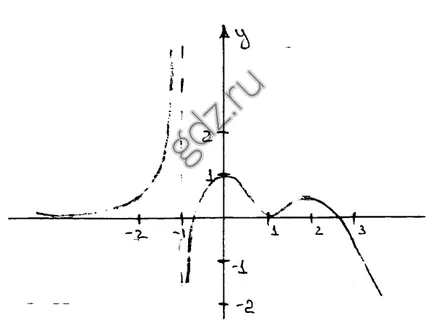
30.12 Определяне монотонността на функцията пространства:
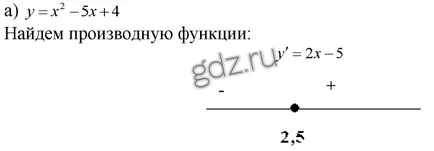

30,13 Определя монотонността на функцията пространства:
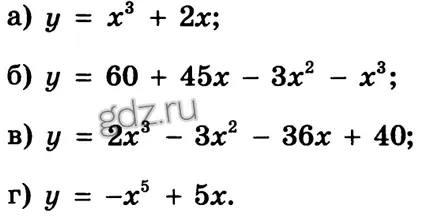



30.14 Изследване на функция на еднообразието:

30.15 Изследване на функция на еднообразието:


30.16 Изследване на функция на еднообразието:


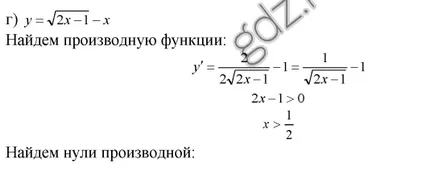

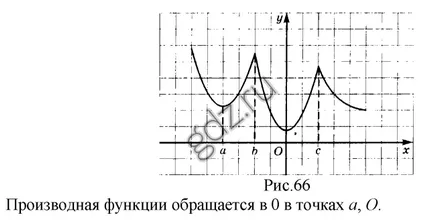
30,17 Според графиката на у = е (х), показано в дадена фигура определи точката, в която неговото производно е равно на 0:
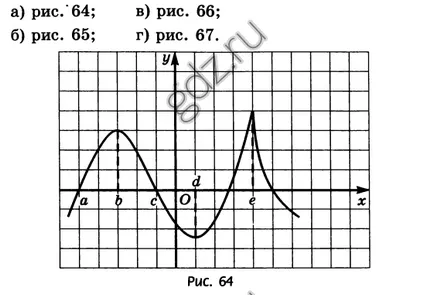
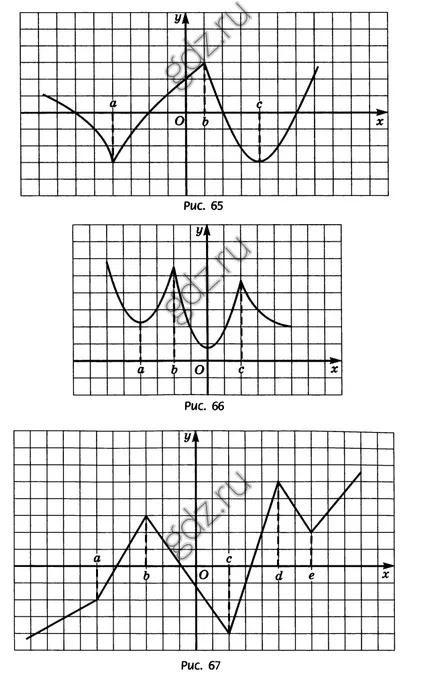
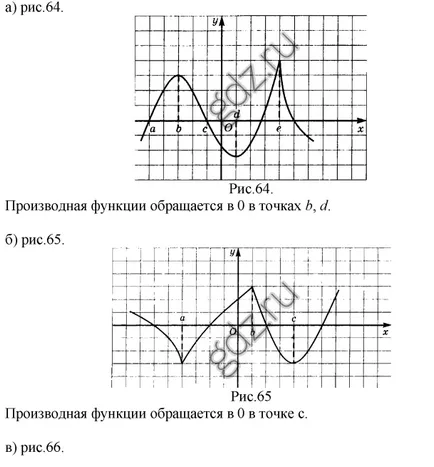
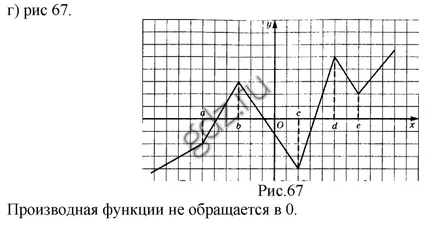
30,18 Според графиката на у = е (х), е показано на фигурата, да определи точката, в която е '(х) не съществува:

30.19 Колко минимални точки има функция у = е (х), графиката на която е показана на фигурата:

30,20 Колко максимални точки е функция у = е (х), графиката на която е показана на фигурата:

30,21 Използвайки данните от производно F '(х), показани в таблицата указва:



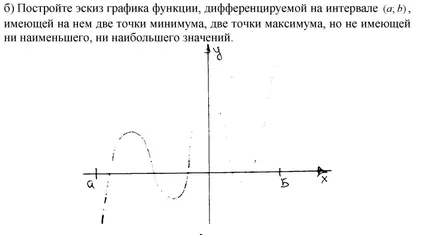
30.23 Може да има само един екстремум точка:

30.24 при какви стойности за дадена функция има една фиксирана точка:

30,25 график производно е показано на фигура (222-223 см ..) определя дали функция у = F (х) екстремум точки:

30,26 Намерете най-екстремалната точки на дадена функция, както и да определи техния характер:


30,27 Намерете най-екстремалната точки на дадена функция, както и да определи техния характер:

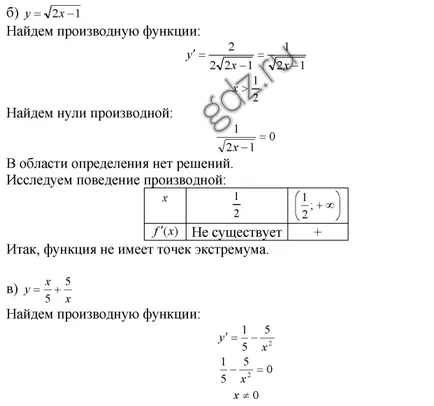

30,28 Намерете най-екстремалната точки на дадена функция, както и да определи техния характер:
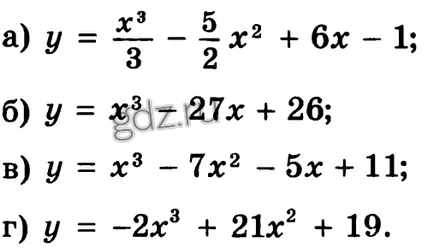

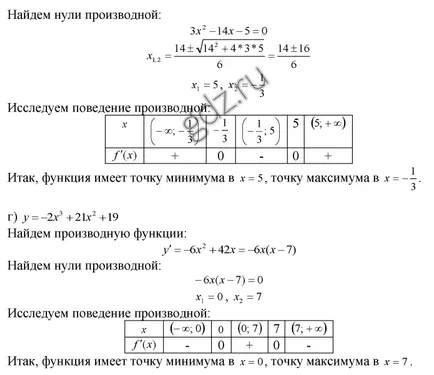
30,29 Намерете най-екстремалната точки на дадена функция, както и да определи техния характер:
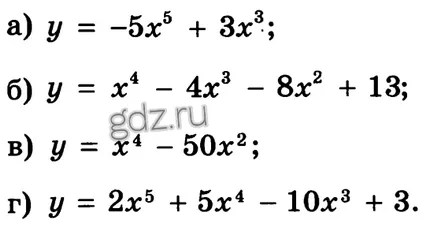


30,30 Намерете най-екстремалната точки на дадена функция, както и да определи техния характер:
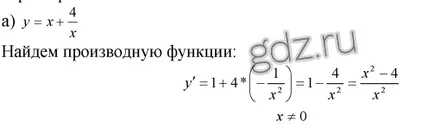

30,31 Намерете най-екстремалната точки на дадена функция, както и да определи техния характер:


30,32 Намерете най-екстремалната точки на дадена функция, както и да определи техния характер: