Глава 4 на втория и третия закон на термодинамиката

Ентропия (от grech.entropia- обрат, трансформация) - концепцията за първи път е въведена vtermodinamike да се определи мярка за необратимо разсейване на енергия. Ентропията vstatisticheskoy физика - мярка на вероятността за реализиране на макроскопско състояние, vteorii информация - мярка за несигурността на експеримента (тест), който може да има различни резултати. Тези тълкувания на ентропия имат дълбока вътрешна връзка.

1 ентропията. Термодинамични ентропия смисъл

По същество всички процеси в макросистеми са необратими.

Възниква въпросът: каква е причината за необратимост? Това е особено странно, като се има предвид, че всички закони на механиката са обратими във времето. И все пак, никой не е виждал, например, да се прекъсне една ваза спонтанно възстановени от отломките.

Решението на този сложен проблем дойде с откриването на нов термодинамична количество - ентропия - и разкриване на неговото физическо значение.

Концепцията за ентропия за първи път е въведен от Р. Клаузиус през 1862. Той е един от най-удивителните открития, направени "на върха на писалката", т.е. теоретично.

Въпреки това, както и липсата на инструменти, които ще измерват ентропията на веществото, това понятие се оказа изключително ползотворно.

ентропия

въведено чрез елементарно нарастване както

Необходимо е да се обърне внимание на функцията на тази формула. Както е известно,

не нарастването на функция, но след разделянето на температурата, Оказва се оказва нарастването на функция (ентропия). За разлика от топлина, ентропиясъщата функция като температура състояние, вътрешна енергияили налягане. Отоплителната системаТова зависи от прехода от началното до крайното състояние, нарастването на ентропиятанапълно независими от процеса, но само на началните и крайните състояния.

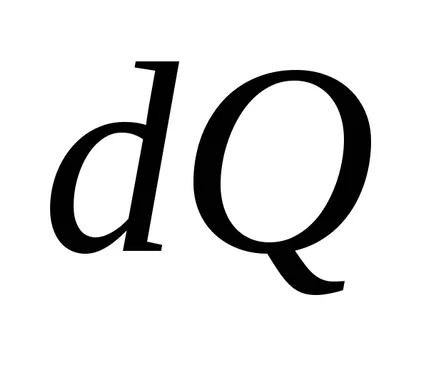
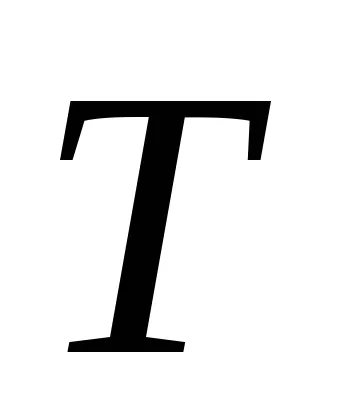
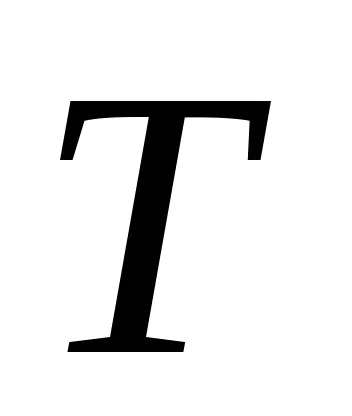
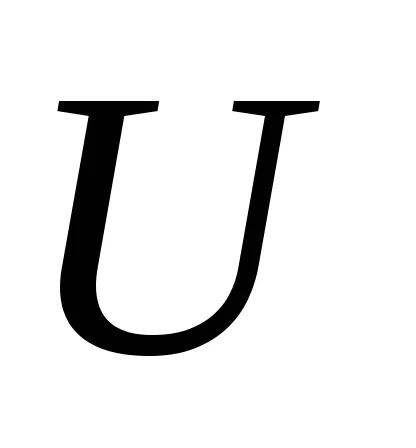
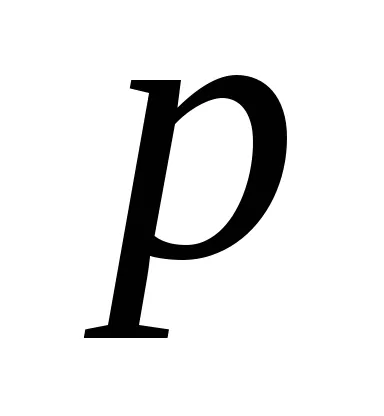
По този начин, при равновесие при температура на пренос на топлина

начално количество топлина е равна на

.

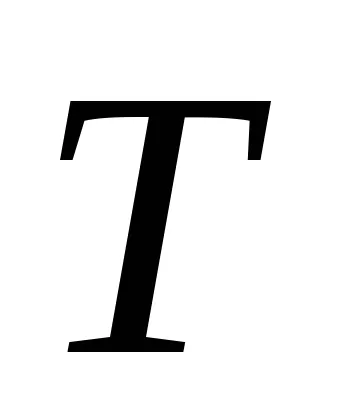
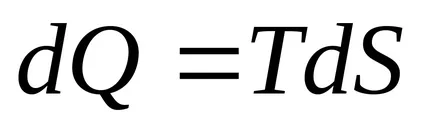
Първият закон на термодинамиката може да се запише като:

Нека първоначалното състояние на организма с температура

и наляганеентропия е, след това, съгласно (4.1) за определяне на ентропиятав друго състояние, като температуратаи наляганеНие трябва да отидем в това състояние, като се започне от всеки процес, равновесие, непрекъснато преминаване на малко количество телесна топлинапри подходящи температури.

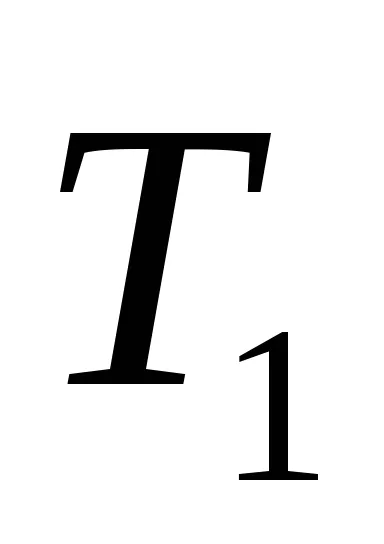
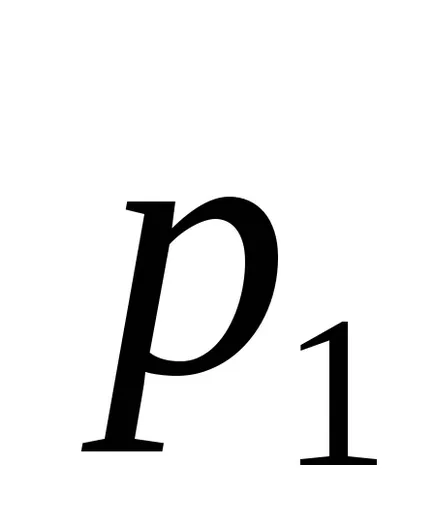
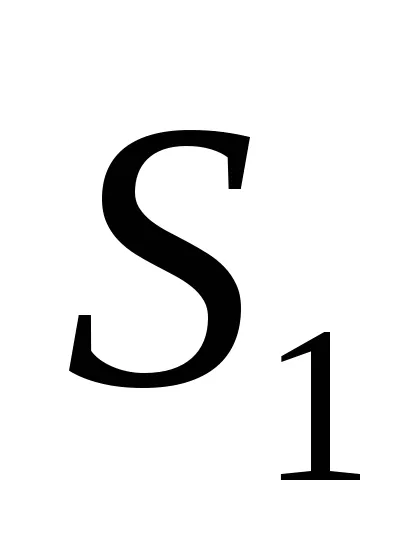
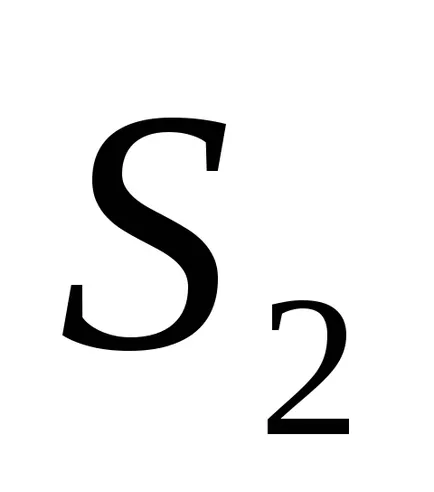
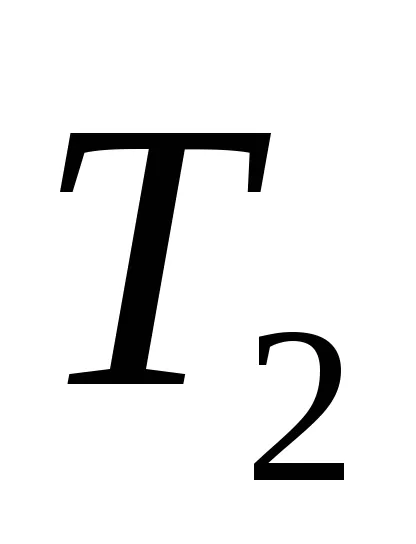
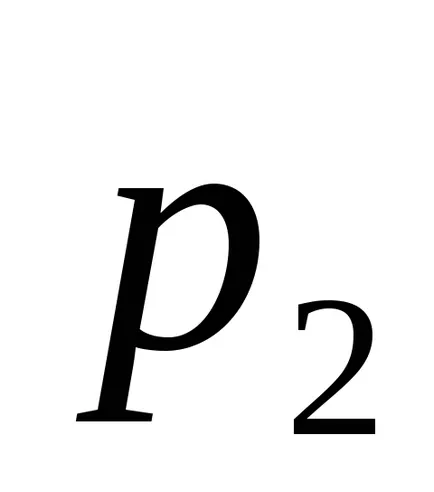
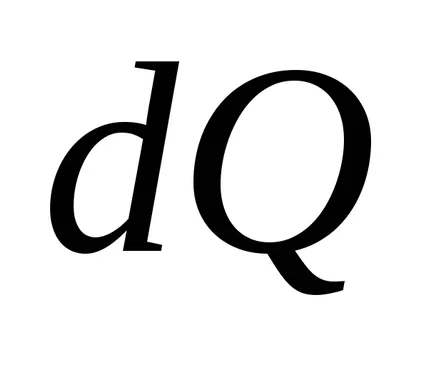
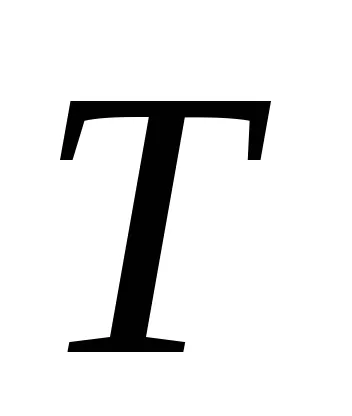
Тогава ентропията

Тя се изчислява по формулата

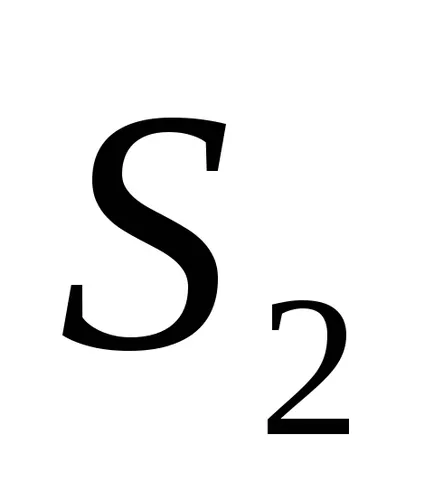
По-специално, за процеса на изотермични (

)

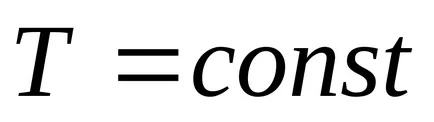
Тъй ентропията е функция от състоянието, интеграл (4.3) не зависи от формата на кривата представлява процес, но определя само от началните и крайните страни, т.е. граници на интеграция.

1) ентропията - стойността на добавката: ентропията на система от няколко тела, е сумата на ентропията на всеки орган

.

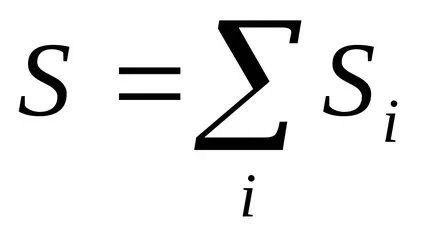
2) равновесие обработва без топлопредаване ентропията не се променя.

В адиабатен процес

.

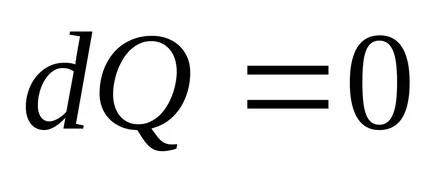
Следователно, съгласно формула (4.1) в равновесие адиабатно процеса

и по този начин. В тази връзка на процеса на адиабатно изоентропен равновесие се нарича още.

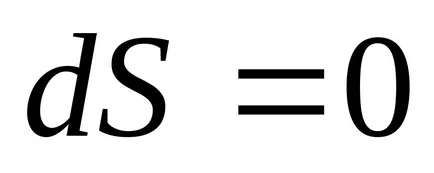
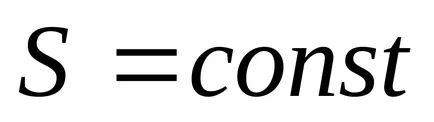
3) при постоянен обем, ентропията е монотонно нарастваща функция на вътрешната енергия на тялото.

В действителност, когато

имаме:, така че. но температуратавинаги положителен. Ето защо, ако, след това.

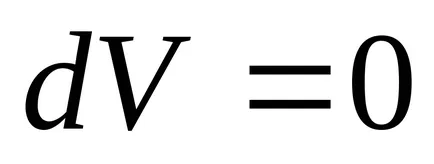
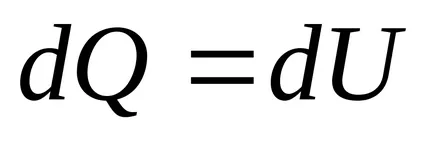
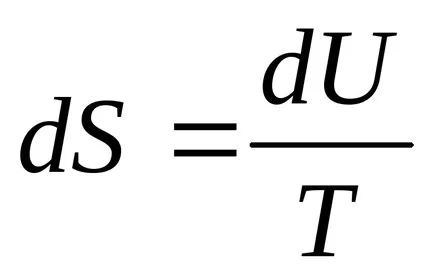
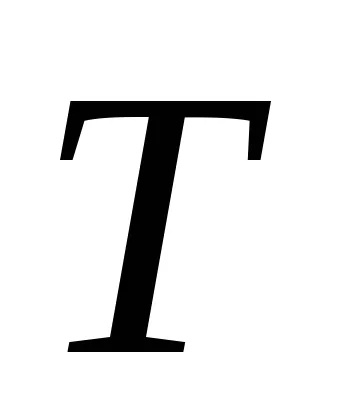
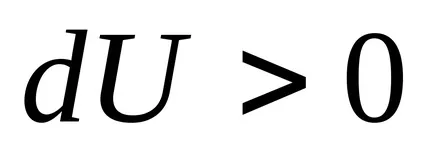
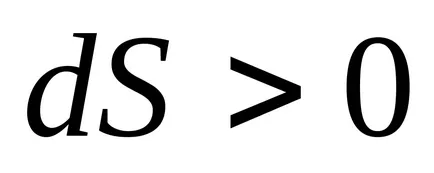
4) ентропията се определя само до произволна константа.

В действителност, според (4.3) можем да изчислим само разликата в ентропии

. Тази разлика не се променя чрез добавяне на ентропията на произволна константа.

5) Насочване вътрешен енергиен като функция на силата на звука и ентропията

напълно определя термодинамичните свойства на хомогенна тяло.

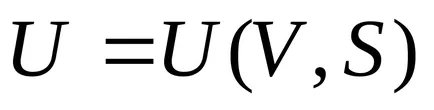
В действителност, според правилото за диференциране на функция на две променливи

.

Като се има предвид (4.2), че

,

Тези уравнения определят температурата и налягането на вътрешната енергия

, акоопределя като функция от обема и ентропията.

Имайте предвид, че равенството

Това е най-общото определение за температура, справедливо и за двете класически и квантови системи.

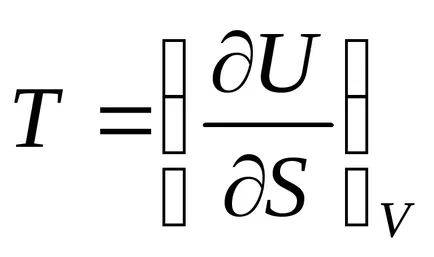
абсолютна температура

- Енергийна мярка за случаен движение на частиците.